钦定四库全书
　历算全书卷五十七
　　　　　　　　　　　　　宣城梅文鼎撰
　几何补编卷一
四等面形算法
　　　　　　　　　　　先算平三角形平三角形
　　　　　　　　　　　三边同者求中得中长线
　　　　　　　　　　　(乙/甲)其三之一即内容平圆

　　　　　　　　　　半径(心/甲)其三之二即外切
　　　　　　　　　　圆之半径(乙心或/心丙)
　
　
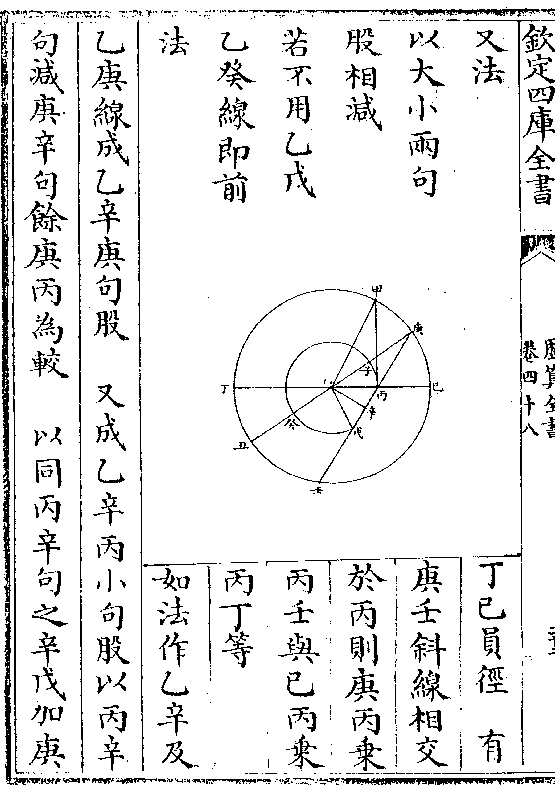
又法以边半之(丙/甲)自乘得数(丙庚/方)取其三之一开方(甲/壬)
(小/方)得容圆之半径(壬癸或甲癸/俱与心甲等)又取自乘数(丙庚/方)三分
加一(丙庚方加/壬甲小方)并而开方得外切圆之半径(丙/心)
论曰三边角等则半边之角六十度(丙心/甲角)其馀角三十

度(心丙/甲角)内容圆半径为三十度之正弦(心/甲)外切圆半径
如全数(丙/心)其比例为一与二故内容圆半径(心/甲)正得外
切圆半径(丙/心)之半也(此论可解/前一条)
形内丙心甲与乙心丁两小句股形相等又并与乙甲
丙大句股形相似(何则乙角丙角并分原等角之半丁/甲等为正角则三角皆等而边之比)
(例/等)而大形之句(丙/甲)既为其弦(乙/丙)之半则小形之句(心丁/亦即)
(心/甲)自必各为其弦(心乙亦/即心丙)之半故知心甲(原同/心丁)为乙甲
之半也

心甲既为心丙之半则心甲一心丙必二而丙戊必三
矣(乙甲/同)何也以乙心与丙心同为二心甲与心戊同为
一也联心乙二与心甲一岂不成三
今以内圆半径为股(心/甲)外圆半径为弦(心/丙)三边之半为
句(丙/甲)成心甲丙句股形则心丙自乘内(弦/幂)有心甲(股/幂)及
甲丙(句/幂)两自乘之积也而心甲股与心丙弦既为一与
二之比例则心甲之幂一心丙之幂必四也以心甲股
幂一减心丙弦幂四其馀积三即丙甲句幂矣故心甲

之幂一则丙甲之幂三心丙之幂四今先得边故以丙
甲三为主而取其三之一为心甲股幂又于丙甲三加
三之一为四即成心丙弦幂也(此论可解/后一条)
　以上俱明三等边平面之比例
今作四面等体求其心
法自乙顶向子向甲剖切之成乙子甲三角面
　　　　　　　　　　心者面之心中者体之心
　　　　　　　　　　前图所谓心者面之心也今

　　　　　　　　　　所求者体之心即后图所谓
　　　　　　　　　　中也故必以剖而后见
　　　　　　　　　　次求甲丑线
　　　　　　　　　　乙子边平分于丑从丑向甲
　　　　　　　　　　得垂线此丑甲垂线在体中
　　　　　　　　　　必小于乙甲在外之垂线故
乙甲如弦丑甲如股乙丑如句也法以甲乙弦自乘内
减乙丑句幂馀为股幂开方得丑甲

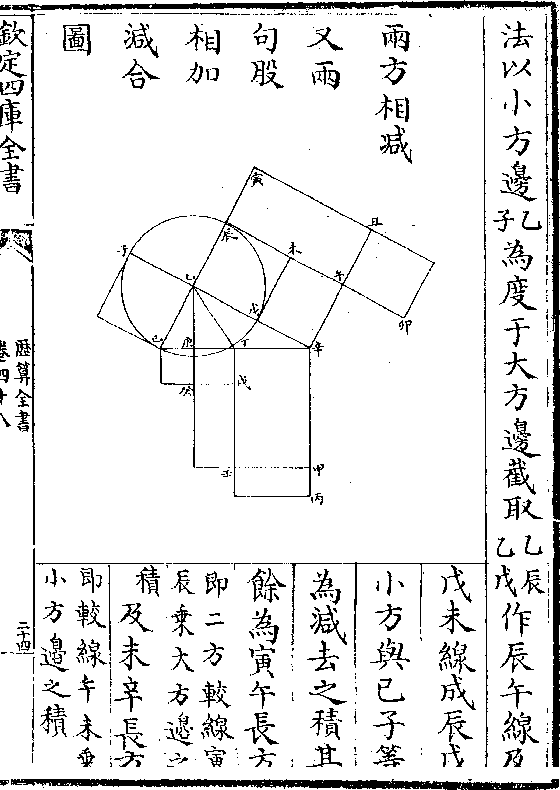
又法准前论乙丑之幂三(即丙甲皆/半边故)则乙甲之幂九(乙/甲)
(三倍大于心甲故心/甲幂一则乙甲幂九)以三减九馀六亦即甲丑股幂矣
以开方得甲丑
捷法倍原半边(甲/丙)自乘数以开方得(甲/乙)中垂线　或半
原边(丙/己)自乘之数开方亦得(甲/丑)　丙甲之幂三(乙丑/同)则
甲丑之幂六而丙己之幂十二也(甲丑与丙己幂积/之比例为一与二)
次求心中线
捷法但半心甲自乘即心中幂

论曰心甲与心中犹甲丑与乙丑也甲丑幂与乙丑幂
为六与三则心甲与心中之幂亦如二与一
又捷法心中之幂一心甲之幂二则乙丑之幂六(即丙/甲)
而心丙之幂八(亦即/乙心)俱倍数
但以半边(乙丑或/丙甲)之幂取六之一即心中幂开方得心
中即四等面形内容小浑圆之半径也(心中线者即各/面之心至体心)
(也故为内容/小浑圆半径)
以心中之幂一(句/)加乙心之幂八(股/)并之为弦幂九开

方得中乙(或中子或用前总图则/为甲丙为甲己并同)是即四等面形外切浑圆之
半径也外切圆之幂九(中/乙)内切圆之幂一(心/中)得其根之比例为
三与一故四等面形内容浑圆之径一则其外切浑圆之径三
又捷法但以乙丑半边之幂加五(即二/之一)为中乙(或中/子等)幂
开方得外切圆之半径(盖乙丑之幂六中乙之幂/九其比例为一有半也)
　　　　　　　　　　此四边不等形(又为三角/立锥形)为
　　　　　　　　　　四等面形四之一各自中切
　　　　　　　　　　至边线成此形其底三边等

即四等面形之一面其高为中心即内容小浑圆之半
径其中乙等三楞线三倍大于中心之高即外切浑圆
之半径
取四等面形全积捷法
先取面幂(即前图乙己丙平面/依前比例求其幂)以内容圆半径(心/中)乘之
得数四因三归见积
法曰丙甲半边之幂三则甲乙中长之幂九开方得中
长(乙/甲)以乘丙甲得乙己丙三等边之幂积即四等面形

之一面也
次求本积四之一(即各面辏心剖/裂之形如右图)
丙申半边之幂六则中心之幂一开方得中心高以乘
所得面幂而三分取其一即为四等面形四之一于是
四乘之即为全积也
又捷法以丙甲乘心甲又以中心乘之即得本形四之
一(即同三除以心甲为/乙甲三之一故也)
此带纵小立方形与右图四等面形四之一等积

　　　　　　　　　　又捷法以丙己全边(亦即/丙乙)乘
　　　　　　　　　　乙心再以中心乘即得本形
　　　　　　　　　　全积(乙心为心甲之倍数丙/己为丙甲之倍数用以)
(相乘则得丙甲乘/心甲之四倍数也)
边设一百
依上法求容
　　　　　　　　丙己边一百其幂一万丙甲半边五
　　　　　　　十其幂二千五百三因之得七千五百

为乙甲中垂之幂(丙甲股幂减丙己弦幂得/句幂也丙己亦即丙乙)　平方开
之得八十六(六○/二五)为乙甲其三之一得二十八(八六/七五)为
心甲　其三之二得五十七(七三/五○)为心乙　又置丙甲
幂二千五百取六之一为心中幂得四百一十六六六
不尽　开方得心中之高二十零四一二四亦即内容
浑圆之半径
依上法以丙己全边一百乘乙心五十七(七三/五○)得五千
七百七十三半　又以心中二十零(四一/二四)乘之得全积

一十一万七千八百五十一弱(与历书/微不同)
　　　　　　　　　　四等面体求心捷法
　　　　　　　　　　准前论心中幂一则心甲幂
　　　　　　　　　　二中乙幂九乙丑幂六以句
股法考之则中甲与中丑之幂俱三也
何也心中甲句股形以中甲为弦故心中句幂一心甲
股幂二并之为中甲弦幂三也而乙中丑句股形以中
丑为句故乙中弦幂九内减乙丑股幂六其馀为中丑

句幂亦三也
由是徵之则中丑与中甲正相等但如法求得甲丑线
折半得中点即为体心
又捷法取乙丑幂(即原设边/折半自乘)半之为中丑幂开方得中
丑亦得甲中(或乙子全边自乘取八/之一为甲中幂亦同)
中丑即原边乙子距体心之度甲中即原边丙己距体
心之度而中为体心
想甲点在丙己边折半之处今从侧立观之则线化为点

　　　　　　　　　　　而丙己与甲成一点故从丙
　　　　　　　　　　　己原边依楞直剖至乙子对
　　　　　　　　　　　边即成甲丑线其线即所剖
　　　　　　　　　　　面之侧立形
　
　　　　　　　　　　　此图即前图甲丑线所切之
　　　　　　　　　　　面盖面侧视则成线矣

　　　　　　　　　　原设四等面全形今依子丑
　　　　　　　　　　乙楞剖至甲则成纵剖图故
　　　　　　　　　　甲点内有丙己线若依丙甲
　　　　　　　　　　己楞剖至丑则成横剖图故
丑点内有子乙也
纵剖有三依子乙楞剖至甲而平分丙己边于甲一也
依丙乙楞剖而平分子巳边二也依己乙楞剖而平分
子丙边三也

横剖亦三依丙己楞剖至丑而平分子乙边于丑一也
依子丙边剖而平分乙己边二也依子巳楞边剖而平
分丙乙边三也其所剖之面并相似皆以中点为三对
角垂线相交之心
一率　一一七八五一　　　例容
二率　一○○○○○○　　例边之立方积
三率　一○○○○○○　　设容
四率　八四八五二九○　　设边之立方积

开方得根二百○四弱为公积一百万之四等面体楞
与比例规解合
若商四数则其平廉积四十八万长廉积九千六百其
隅积六十四共得四十八万九千六百六十四不足四
千三百七十四为少百分之一弱故比例规解竟取整
数也
　计开
四等面诸数

边一百
积一十一万七八五一
积一百万
边二百○三九六
内容浑圆半径二十○(四一/二四)
内容浑圆全径四十○(八二/四八)
外切浑圆半径六十一(二一/○○)
外切浑圆全径一百念二(四二/○○)

互剖求心之图
　　　　　　　　　　设边一百其幂一万(丙己乙/子乙丙)
　　　　　　　　　　(乙己子丙子己并同为/外切浑圆径幂三之二)
　　　　　　　　　　半边五十其幂二千五百(丙/甲)
　　　　　　　　　　(甲己乙丑丑子等并/同为边幂四之一)
　　　　　　　　　　斜垂线之幂七千五百(乙心/甲子)
　　　　　　　　　　(角甲丙亢丑己氐丑/并同为边幂四之三)
　　　　　　　　　　其根八十六六○二五

　　　　　　　　　　斜垂线三之一二十八八六
　　　　　　　　　　七五其幂八百三十三三三
　　　　　　　　　　(即外切浑圆径幂十八/之一为边幂十二之一)即各
　　　　　　　　　　面内容平圆半径(心甲角甲亢/丑氐丑并同)
斜垂线三之二五十七七三五○其幂三千三百三十
三三三(乙心子角丙/亢己氐并同)
内容浑圆半径二十○四一二四其幂四百一十六六
六不尽(为边幂二十四之一即/外切浑圆三十六之一)即分体中高(心中角中/亢中氐中)

(并/同)　若内圆全径之幂则一千六百六十六六六(为边/幂六)
(之一外切浑圆/径幂九之一)
外切浑圆半径六十一二三七二其幂三千七百五十
即分体之立面楞(乙中子中丙/中己中并同)四因之为浑圆全径幂
一万五千其径一百二十二四七四四
又外切正相容之立方其幂五千为四等面边幂之半
即斜方之比例又为外切浑圆径幂三之一
一率　外切浑圆径一百二十二四七四四

二率　四等面之边一百
三率　浑圆径一百
四率　内容四等面边八十一六四九六
又捷法浑圆径幂一万五千则内容四等面边幂一万
或内容立方面之斜亦同为浑圆径幂三之二
若设浑圆径一百其幂一万则内容四等面边之幂六
千六百六十六六六亦三之二也
平方开之得八十一六四九六为四等面边即内容立

方之斜内容立方面幂三千三百三十三三三为浑圆
径幂三之一即方斜之半幂亦即四等面边幂之半
平方开之得五十七七三五○是为浑圆径一百内容
立方之边亦即浑圆内容立方立方又容小圆之径
若于四等面内又容浑圆则其径幂一千一百一十一
一一为浑圆径幂九之一为四等面幂六之一立方面
幂三之一
开得平方根三十三三三不尽(幂九之一则其/根必三之一也)为内容

小浑圆之径以径乘幂得三万七千○三十七为径上
立方积　以十一乘十四除得二万九千一百○○半为
圆柱积　柱积取三之二得一万九千四百为小浑圆
积得大浑圆二十七之一　以小浑圆积二十七因之
得五十二万三千九百为四等面外切大浑圆积(即径/一百)
(之浑圆/积也)
互剖求心法
凡四等面体任以一尖为顶则其垂线为自尖至相对

之平面心(亦即平面/容圆之心)而以馀三尖为底其垂线至底之
点旁距三尖皆等(即乙心丙心己心三线之距心皆等/而以子尖为顶其垂线为子中心其)
(底为乙丙己平/三角面馀仿此)此为正形(各尖皆可为/顶其法并同)若以子中心垂
线为轴而旋之则成圆角体
凡四等面体任平分一边而平分之点为顶以作垂线
则其垂线自此点至对边之平分点而以对边为底
底无面但有边底边与顶边相午直正如十字形
假如以子乙边平分于丑以线缀而悬之则其垂线至

所对丙己边之平分正中为甲点其线为丑中甲而子
乙边衡于上则丙己边纵于下正如十字无左右之欹
亦无高下之微差也
若以丑中甲垂线为轴旋之则成圆柱体
凡四等面体以其边为斜线而求其方以作立方则此
立方能容四等面体
何以知之曰准前论以一边衡于上而为立方上一面
之斜则其相对之一边必纵于下而为立方底面之斜

　　　　　　　　　　矣又此二边之势既如十字
　　　　　　　　　　相午直而又分于上下为立
　　　　　　　　　　方上下两面之斜线然则自
上面之各一端向底面之各一端联为直线即为四等
面之馀四边亦即立方馀四面之斜如此则四等面之
六边各为立方形六面之斜线而为正相容之体
如前所论圆角体圆柱体虽亦能容四等面形而垂线
皆小于圆径故不得为正相容

捷法四等面之边自乘折半开方即正相容之立方根
(即弦倍/句股意)设边一百其幂一万折半五千即为立方一面
之积求其立方根得七十○七一○六即丑中甲垂线
之高
若以此作容四等面之圆柱则其高七十○七一○六
同立方之方根而其圆径一百同立方面之斜此圆柱
内可函立方
其乙中子中等为自四等面体心至各角之线又为立

方心至各角之线又为外切浑圆之半径又为四等面
分为四体之楞线又为立方分为六方锥之楞线
又捷法以四等面之边幂加二分之一开方即外切正
相容之浑圆径亦即立方体内对角线(如自乙/至震)折半为
自心至角线　四等面设边一百其幂一万用捷法二
分加一得一万五千为外切正相容之浑圆全径幂开
方得一百二十二四七四四为浑圆全径折半得六十
一二三七二为浑圆半径

立方内容四等面图
　　　　　　　　　　设立方边一百其积百万内
　　　　　　　　　　容四等面边一百四十一(四/二)
　　　　　　　　　　(一/三)其积三十三万三千三百
　　　　　　　　　　三十三(三三/三三)为立方积三之
一乾坤震巽立方(乾丙坤己乙巽子震/与中心之丑甲同高)内容子乙丙己
四等面为立方积三之一
何以明之凡锥体为同底同高之柱体三之一今自立

方之乙角依斜线剖至丙巳成乙丙巳巽三角锥以丙
巳巽立方之半底为底又自子角斜剖至丙巳成子丙
巳震锥以丙巳震立方之半底为底合丙半底则与立
方同底矣而子震与乙巽之高即立方高也是此二锥
得立方三之一矣
又自子乙斜线斜剖至巳角成倒锥以子乙坤立方之
半顶为底以坤巳立方高为高又自子乙斜剖至丙角
亦成倒卓之锥以子乙乾立方之半顶为底以乾丙立

方高为高与前二锥同亦三之一也
合此二锥共得立方三之二则其馀为子乙丙巳四等
面体者必立方三之一矣
准此论之凡同边之八等面积四倍大于四等面积何
以知之以此所剖之四锥体合之则为八等面之半体
皆以剖处为面而其边其面皆与四等面等是同边之
体也而八等面之半体既倍大于四等面则其全体必
四倍之矣

设八等面边一百四十一(四二/一三)与四等面同边则八等
面之积一百三十三万三千三百三十三(三三/不尽)为四等
面之四倍
若设四等面边一百则其外切之立方面幂五十立方
根七十○(七一/○六)以根乘幂得立方积三十五万三千五百
五十三四等面积一十一万七千八百五十一为立方
积三之一
推得八等面边一百其积四十七万一千四百○四

　此同边之比例
若立方内容之八等面则其积为立方内容之四等面
二之一何以知之八等面与立方同高则其积为立方
六之一故也
设立方边一百内容八等面边七十○(七一/○六)其积一十
六万六千六百六十六为四等面之半若设立方边七
十○(七一/○六)则内容八等面积五万八千九百二十五半
其边五十

　　　　　　　　　　四等面体又容小立方小立
　　　　　　　　　　方内又容小四等面体则内
　　　　　　　　　　容小立方径为外切立方三
　　　　　　　　　　之一内小四等面在小立方
　　　　　　　　　　内其径亦为四等面三之一
而其积皆二十七之一
何以知之凡三等边平面之心皆居垂线三之一假如
子巳丙为四等面之一面其平面之心必在癸而子甲

垂线分三之一为癸甲其馀三面尽同而内容之小立
方必以其下方之两角纵切子巳丙之癸心及乙己丙
之壬心其上方之两点必横切于子乙己之卯心及子
乙丙之申心而立方内容之小四等面亦必以其四角
同切此四点也今壬癸两点既下距丙己线为其各斜
垂线三之一而卯申两点又上距子乙线之斜垂线亦
三之一则其中所馀三之一必为立方所居也而内小
立方不得不为子乙与丙己相距线三之一矣

问癸点为三之一者斜面之垂线也小立方者直立线
也何以得同为三之一乎答曰癸点所居三之一虽在
斜面而子乙纵线与丙己横线上下相距必有垂线直
立于其心此直立垂线即前图之甲丑与外切立方线
同高者也丑甲中垂线以上停三之一之上点与卯申
平对以下停三之一之下点与壬癸平对依句股法弦
与股比例同也然则丑甲线之中停即小立方之所居
矣

又丑甲者即外切立方之高也故知小立方径为外切
立方径三之一
又小四等面在小立方内以其边为小立方之斜而纵
横边相午对如十字其中心亦以丑甲线之中停为其
轴其斜面之势一切皆与大四等面同而丑甲者亦大
四等面之轴也小四等面之中轴既为丑甲三之一其
馀一切皆三之一矣
夫体积生于边者也边为三之一者面必为九之一体

必为二十七之一无疑也
准此论之浑圆在四等面内者亦必为外切浑圆二十
七之一其径亦三之一也何也浑圆之切点与小立方
小四等面之切点并同也
以此推知小立方与小四等面在大四等面内或居小
浑圆内以居大四等面内其径积并同
求体积
浑圆径一百其径上立方一百万依立圆法以十一乘

十四除得七十八万五千七百一十四为圆柱积仍三
分取二得五十二万三千八百○九为浑圆积
内容立方面幂三千三百三十三(三/三)其边五十七(七三/五○)
以边为高乘面得一十九万二千四百五十○为内容
立方积
内容四等面体边幂六千六百六十六(六/六)其边八十一
(六四/九六)
依前论四等面体为立方三之一得六万四千一百五

十○为四等面积
立方内容小浑圆以立方之边为径五十七(七三/五○)依立
圆法以立方积十一乘十四除得一十五万一千二百
一十为圆柱积取三之二得一十○万○八百六十六
为小立圆积
四等面内容小浑圆径幂一千一百一十一(一/一)其径三
十三(三/三)以径乘幂得径上立方积三万七千○三十七
以十一乘十四除得二万九千一百○半为圆柱积又

三分取一得一万九千四百为立方内之四等面内容
小浑圆积为大浑圆积二十七之一若先有内小浑圆
积但以二十七因之得大浑圆积
依此论之凡浑圆内容立方立方内又容四等面体四
等面内又容小浑圆其内外相似之大小二体皆二十
七之比例也
又捷法用方斜比例
立方面之斜设一百其幂一万则其方幂五千用三

　　　　　　　　　　因之得一万五千开方得立
　　　　　　　　　　方对角斜线即为外切浑圆
　　　　　　　　　　全径
　
立方面之斜一百即立方内容四等面之边
立方体对角斜线一百二十二(四七/四四)即立方外切浑圆
之全径亦即四等面外切浑圆全径半之得六十一(二/三)
(七/三)即立方外切浑圆半径亦即立方体心至各角之线

亦即四等面体心至各角之线
八等面形图注
第一合形
　　　　　　　　　　甲丁　甲丙　甲己　甲戊
　　　　　　　　　　丁丙　丙己　己戊　戊丁
　　　　　　　　　　戊乙　己乙　丁乙　丙乙
　　　　　　　　　　以上形外之楞凡十有二即根
数也其长皆等

或设一百为一楞之数则十二楞皆一百也
甲丁戊　甲戊己　甲己丙　甲丙丁　丙丁乙
己丙乙　戊己乙　丁戊乙
以上形周之分面凡八皆等边平三角形也其容积其
边皆等
或设一百为边数则三边皆一百而形周之分面八皆
三边边皆一百也
第二横切形(二/)

　　　　　　　　　　甲丁丙己戊为上半俯形
　　　　　　　　　　丁丙己戊乙为下半仰形
　　　　　　　　　　右二形各得合形之半皆从
　　　　　　　　　　丁戊楞横剖至己丙
　　　　　　　　　　一俯一仰皆方锥扁形丁丙
　　　　　　　　　　己戊为方锥之底其边皆等
　　　　　　　　　　其从四角凑至顶之楞皆与
底之边等

第三直切形(四/)
　　　　　　　　　　从甲尖依前后楞直剖过丁
　　　　　　　　　　己至乙尖成左右两形
　　　　　　　　　　从甲尖依左右楞直剖过丙
　　　　　　　　　　戊至乙尖成前后两形
　　　　　　　　　　此四形者一切皆与仰俯二
　　　　　　　　　　形同但彼为眠坐之体故为
方锥(仰者即倒/卓方锥)而此则立体即如打倒方锥之形也

第四横切之面一直切之面二
　　　　　　　　　因横剖得正方平面在立方锥以此
　　　　　　　　　为底倒方锥以此为面在合形则为
　　　　　　　　　腰围其己丁及丙戊两对角斜线相
　　　　　　　　　交于心即两直切之界也(心即合/形中心)
　　　　　　　　　因直剖得斜立方面二其己丁及戊
　　　　　　　　　丙横对角线即横切之界其从甲至
　　　　　　　　　乙垂线即直剖之界如立面在前后

　　　　　　　　　互剖之形则此线为左右直剖之界
　　　　　　　　　彼此互为之也亦即为全形之中高
　　　　　　　　　径线
　　　　　　　　　以此知八等面之中高线为方斜之
　　　　　　　　　比例
　
　
第五分形

　　　　　　　　　　因横剖及两直剖分总形为八皆
　　　　　　　　　　三角锥形也
　　　　　　　　　　皆以等边平三角形面为锥形之
　　　　　　　　　　底而以横直剖线相交处之点为
　　　　　　　　　　其锐顶即合形之中心也
　　　　　　　　　　其自顶心至角之楞皆等皆边线
　　　　　　　　　　之方斜比例也(底线为方则此/线为其斜之半)而
　　　　　　　　　　此楞线又即为八等面形之外切

　　　　　　　　　　　圆之半径
　
　
　　　　　　　　　　　设己戊边一百其幂一万则心戊
　　　　　　　　　　　楞之幂五千(倍戊庚半边之/幂为半斜幂也)
　　　　　　　　　　　戊心之幂五千内减戊庚幂二千
　　　　　　　　　　　五百则其馀二千五百为心庚之
　　　　　　　　　　　幂故心庚必与戊庚等

从心顶对己庚楞直剖至庚分形为两则其中剖处成三角平
面
　　　　　　　　　　　己庚者乙己戊等边三角平面之
　　　　　　　　　　　中垂线也其幂为边四之三设边
　　　　　　　　　　　一百之幂一万则己庚之幂七千
　　　　　　　　　　　五百
庚辛者平面三角容圆之半径也得己庚三之一其幂则九之
一也己庚之幂七千五百则庚辛之幂八百三十三(三/三)

辛点即各三角平面之中心
以庚辛幂八百三十三(三/三)减心庚幂二千五百得心辛
幂一千六百六十六开方为心辛即分形之中高也求
得分形中高四十○(八二/四七)
依平面三等边法设边一百其中长线八十六(六○/二五)其
幂积得四千三百三十○(一二/五○)　取平幂三之一得一
千四百四十三(三七/五○)以乘中高得分形积五万八千九
百二十五(三五/一三)　再以八因之得总积四十七万一千

四百○二(八一/○四)与总算合
设八等面之边一百其幂一○○○○即横剖中腰之
正方　半之为每角辏心之线之幂得○五○○○此
线即分形自底角辏顶心之楞(如心戊心/己心乙)又为八等面
形外切浑圆之半径　又半之为分形每面自顶至边
斜垂线之幂(即心/庚)得○二五○○此线即设边之半其
幂为设边四之一
设半边之幂取其三之二为分形中高线之幂(即心/辛)得

○一六六六不尽又为八等面形内容浑圆之半径
捷法取八等面设边之幂六而一为八分体中高之幂
开方得中高
假如设边一百其幂一万则分体中高之幂一千六百
六十六不尽　求其根得四十○(八二/四八)　以中高乘三
角平面幂三除之得分体八因之得全积
又捷法八等面设边之幂取三之二为体内容浑圆之
径幂开方得内容浑圆径折半为八分体中高

假如设边一百其幂一万则内容浑圆之径幂六千六
百六十六不尽　求其根得八十一(六四/九六)　折半为分
体中高
或竟以内容浑圆全径乘设面三角平幂四因三除之
得全积
又捷法　此方斜之比例
八等面设边之幂倍之为体外切圆径幂开方得径以
乘设边之幂(即腰广/平方)得数三归见积

假如设边一百其幂一万其斜如弦弦之幂倍方幂得
二万求其根得一百四十一(四二/一三)　以乘腰广一万得
一百四十一万四千二百一十三　三除之得总积四
十七万一千四百○四
一系　八等面体之边上幂与其外切浑圆之径上幂
　　其比例为一与二(方斜/比例)
一系　八等面体之边上幂与其内容浑圆之径上幂
　　其比例为三与二

一系　八等面体外切浑圆之径上幂与其内容浑圆
　之径上幂　其比例为三与一
准此而知八等面内容浑圆浑圆内又容八等面其浑
圆外切之八等面边或径上幂与内容之八等面边或
径上幂其比例亦必为三与一也
　计开
八等面形诸数
设边一百　其积四十七万一四○四(与历书所/差甚微)

其体外切浑圆之径一百四十一(内外两浑圆之径幂/为三与一其根约为)
(四与七/而强)体内容浑圆之八十一
八等面外切立方径一百四十一(方斜比例也与/外切浑圆同)
八等面内容立方径四十七
内外切大小立方之径之比例为三与一
内外两立方之积之比例为二十七与一
若浑圆内容立方立方内容八等面体八等面体内又
容浑圆则大小两浑圆之径亦若三与一其积亦若二

十七与一
一率　　四七一四○四　　例容
二率　　一○○○○○○　例边之立方
三率　　一○○○○○○　设积
四率　　二一二一三二二　设边之立积
开立方得根一百二十八为公积一百万之八等面根
(与比例/规解合)

　几何补编卷二
二十等面形自腰切之成十等边平面
　　　　　　　　　　先求甲丁　乃十等边平面
　　　　　　　　　　从心对角之线　亦即二十
　　　　　　　　　　分形各三角立体一面之中
垂斜线
法为甲乙(即切形十等边之半在原设/二十等面形边为四之一)与甲丁若十八
度之正弦与全数也(十等边各三十六/度其半十八度)

设边一百　所切十等边平面之边五十　其半甲乙
二十五
一率　十八度正弦　○三○九○
二率　全数　　　　一○○○○
三率　甲乙　　　　　　　二五
四率　甲丁　　　　　　　八○(九○/六一)
用等边三角求容圆法
设边一百　其内容圆半径二十八(八六/七五)为心甲

　　　　　　　　　　以心甲为句二十八(八六/七五)
　　　　　　　　　　其幂八百三十三(三三/二五)
　　　　　　　　　　以甲丁为弦八十○(九○/六一)
　　　　　　　　　　其幂六千五百四十五(七九/七○)
句幂减弦幂馀五千七百一十二(四六/四五)为心丁股幂
开方得心丁七十五(五八/○八)　此即各面切形自各面之
心至切体尖之高也　其切体之尖即原设二十等面
总形之体心为丁点

用后法得乙己丙平面幂积四千三百三十○(一二/五○)
又依三等边角形设边一百(丙/己)　其半五十(丙/甲)　求到
乙甲中长八十六(六○/二五)用其三之一即心甲二十八(八/六)
(七/五)以与丙甲五十相乘得一千四百四十三(三七/五○)为各
等面平积三之一(三因之得/平面幂)
又以丁心七十五(五八/○八)乘之得一十○万九千○九十
一(四三/七二)为二十等面形分切每面至心之积又以二十
乘之得全积

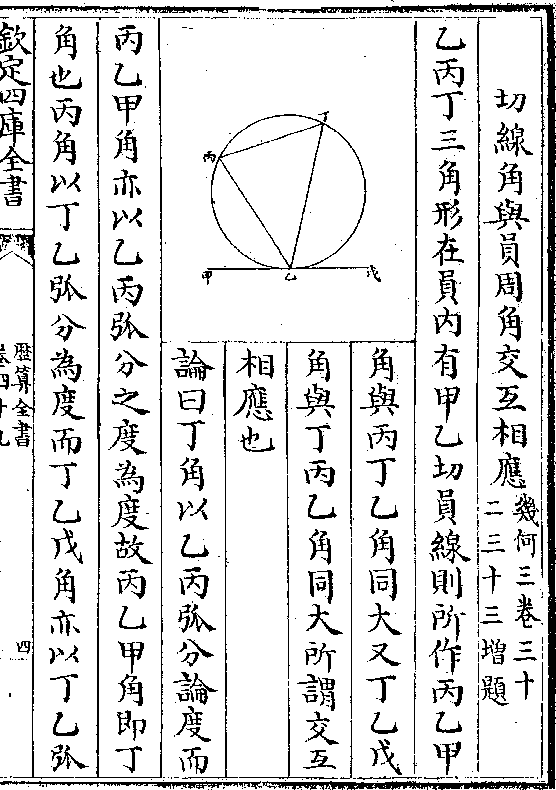依上法求到二十等面全积
设边一百　其积二百一十八万一千八百二十八(查/比)
(例规解差不多惟/测量全义差远)
　按此法以本形分为二十各成三角立锥形而各以
　分形之高乘底取三之一以为分形积然后以等面
　二十为法乘而并之得总积可谓的确不易矣然与
　历书中比例规解及测量全义俱不合何耶
　　计开

二十等面形
设边一百　其每面中长线八十六(六○/二五)
其每面幂积四千三百三十○(一二/五○)
其每面容平圆之心作线至形心之丁七十五(五八/○八)即
心丁　心丁即内容浑圆之半径
其分形各以每面之幂积为底心丁为高各得三角立
锥积一十万九千○九十一(四三/七二)
其立锥积凡二十合之得总积二百一十八万一千八

百二十八
用上法求形内容浑圆
其心丁七十五(五八/○八)即内容浑圆半径(以心丁线与各/平面作垂线而)
(丁点即/体心故)倍之得一百五十一(一六/一六)为内容浑圆全径
置小浑圆径一百五十一零自乘得二万二千八百○
一以十一乘十四除得一万七千九百一十五为圆幂
置内容浑圆之平圆幂一七九一五以圆径一百五十
一取三之二得一百强以乘平圆幂得一百八十○万

二千二百四十九为二十等面内容浑圆之积
置内容圆径一百五十一自乘得(二万二千/八百○一)再乘(三百/四十)
(四万二千九/百五十一)以立员捷法(○五二三五/九八七七)乘之得浑圆积
一百八十○万二千七百二十五
先用密率(十四除/十一乘)得浑圆一百八十万二千二百四十九
　以较立圆捷法所得少尾数四百七十六约为一万
八千之五弱不足为差也
依立圆法以圆率三一四一五九二乘立圆法六而一

得五十二万三五九八为径一百之浑圆积
依法求得立方边五十七(七三/五○)立方积一十九万二四
五○四等面积六万四千一百五十○并合前算
小浑积一○○七六六　若用捷法以浑圆率五二三
五九八乘立方积得数后去末六位亦得一十○万○
七六六
　内容浑圆尚且如此之大况二十等面之形又大于
　内圆乎然则历书之率其非确数明矣

二十等面
一率　　二一八一八二八　　例容
二率　　一○○○○○○　　例根一百之体积
三率　　一○○○○○○　　设容
四率　　○四五八三三二　　所求根立积
如法算得二十等面之容一百万其根七十七
　比例规解作七十六尚差不多测量全义云二十等
　边设一百其容五二三八○九则大相悬绝矣久知

　其误今乃得其确算己未年所定之率以两书酌而
　为之究竟不是今乃得之可见学问必欲求根也
二十等面分体之图
　　　　　　　　　　亥子戌为二十等面之一面
　　　　　　　　　　亦即各分体之底
　　　　　　　　　　亥子子戍戍亥皆其边即根
　　　　　　　　　　也半之为亥甲
甲乙丙为横边切处即横切成十等边形之一边

丁为体心亦即切十等边平面之中心
甲乙丙丁即横切十等边平面之分形　心为二十等
面每面之正中　心丁为体周各平面至体心之垂线
亦即分体之中高亦即体内容浑圆之半径　丁亥丁
子丁戌皆分体之楞线乃自各分面角辏体心之棱也
亦即为外切浑圆之半径　丁甲丁丙皆横切平面各
角辏心之线亦即分体各斜面之中垂斜线也
求法以丁甲为股亥甲为句(即根/之半)两幂相并开方得弦

即丁亥也(丁子丁/戌同)
求二十等面外切浑圆之半径
依句股法　以丁甲股八十○(九○/六一)自乘幂六千五百
四十五(七九/七○)　亥甲句五十○自乘幂二千五百　相
并为亥丁弦幂九千○四十五(七九/七○)　平方开之得亥
丁九十五(一○/五二)为外切浑圆半径　亦即二十分形自
其各角辏心之棱　倍之得一百九十○(二一/○四)即外切
浑圆全径

　计开二十等面体诸数
设边一百　其容二百一十八万一千八百二十八
其内容浑圆径一百五十一　其外切浑圆一百九十
其每面中心至体心七十五半(即内容浑/圆之半径)
其每面各角至体心九十五(即外切浑/圆之半径)
　计开二十等面体诸用数
设边一百　外切立方之半径八十○(九○/一七)为体心至
边之半径(即寅中卯/中辰中等)

倍之为边至边一百六十一(八○/三四)即外切立方全径
外切浑圆之半径九十五(一○/五六)为体心至各角尖之半
径(即甲中戊/中心中等)
倍之为角尖至角尖一百九十○(二一/一二)即外切浑圆全
径
内容浑圆及内容十二等面之半径七十五(五七/六一)为体
心至各面之半径(即己中/庚中等)
倍之为内容浑圆全径一百五十一(一五/二二)为面至面

内容十二等面之边五十三(九三/四四)
每面之幂四千三百三十○(一二/五○)
二十等面之幂共八万六千六百○二半
分体积一十○万九千○八十四(六/五)为二十等面体积
二十之一
合之得全积二百一十八万一千六百九十三
内容小立方之边八十七(二六/七七)　(以内容立圆径自乘/乏幂取三之一开方)
(得/之)

内容灯体边五十(即原边/之半)
立方内容二十等边算法
　　　　　　　　　　亢卯寅房为立方全径一百
　　　　　　　　　　中寅中卯为半径五十
　　　　　　　　　　寅卯二点为二十等面边折
　　　　　　　　　　半之界
　　　　　　　　　　寅卯线为二十等面边之半
中为体之中心　寅中卯角为三十六度

中寅半径当理分中末之全数　寅卯即理分中末之大分
　　　　　　　　　　　甲戊戊心心甲皆寅卯之倍数即
　　　　　　　　　　　二十等面之边其数六十一(八○三/三九八)
　　　　　　　　　　　甲辰半边三十○(九○一六六/九与寅卯同)
心辰垂线五十三(五二/三三)　半垂线心箕二十六(七六/一六)　甲辰幂
九百五十四(九一/五○)　三因甲辰幂为心辰幂二千八百六十四
(七四五/○不尽)
　计开

立方径设一百　半径五十
理分中末线大分六十一(八○三/三九八)即二十等面之边
论曰以中寅半径五十求寅卯正得理分中末大分之
半而甲戊边原倍于寅卯寅房全径亦倍于寅中是全
数与大分皆倍也故径以全数当寅房全径以理分中
末之大分当甲戊等二十等边之全边也
又立方边设一百(即寅/房径)　半之五十(即中/寅)
内容二十等面之边六十一(八○三三九/八即甲戊等)

面之中垂线五十三(五二三三/即心辰)
中垂线之半二十六(七六一六/即心箕)
面之幂一千六百五十三(九五七八/甲戊心面)
中垂线三之一得一十七(八四一一/即心己)
内容立圆半径四十六(七○八六/即己中)　全径九十三(四一/七二)
二十等面全积五十一万五千○二十六(九五/九七)
约法
立方根与所容二十等面之边若全数与理分中末之

大分　面幂三之一以乘容圆全径得数十之为全积
中垂线三之一心己为句(即平面容/员半径)自乘得句幂三百
一十八(三○四/八四九)以减中寅弦幂二千五百○○馀己中
股幂二千一百八十一(六九五/一五一)开方得己中根四十六
(七○/八六)
二十等面边设一百用理分中末线求其外切之立方
一率　二十等面边六十一(八○三/三九八)
二率　外切立方一百○○

三率　二十等面边一百○○
四率　外切立方一百六十一(八○/三四)
依法求得二十等面边一百其外切立方一百六十一
(八○/三四)与先所细算合
半圆内容正方
法以圆径为三率(丙/丁)　理分中末之小分为二率(庚/辛)
理分中末全线加小分为首率(丁辛为全线再加庚辛/为小分共得为丁庚总)
(线/也)　二三相乘一率除之得四率(丙乙即/甲丁)为全径之小

　　　　　　　　　　分以减全径馀(乙/丁)乃于乙作
　　　　　　　　　　正十字线至圆界(如己/乙)即以
　　　　　　　　　　此线自乘作正方(己/甲)如所求
　
论曰己乙即丙乙与乙丁之中率而丙乙既为乙丁全
径之小分则己乙即大分也而甲乙亦为大分　甲丁
亦为小分矣若自甲作甲戊必与己乙甲乙等而其形
正方

半浑圆内容立方
法以乙甲圆径自乘之幂取其六之一开方得容方根
(丙丁方/丙戊边)
论曰试倍甲丙乙庚半浑圆为全浑圆体亦倍丙丁正
方形作丙己长立方形亦必能容矣然则丙己线在长
　　　　　　　　　　立方形之内为斜线者亦即
　　　　　　　　　　浑圆之径也(与甲乙/径等)
　　　　　　　　　　试于长立方面作戊己斜弦

　　　　　　　　　　则己壬为之句戊壬为之股
　　　　　　　　　　而戊己弦幂内有己壬幂与
　　　　　　　　　　戊壬幂矣
　　　　　　　　　　而丙己线为弦则戊己又为
股丙戊又为句而丙己自幂内又兼有戊己幂及丙戊
幂矣(丙戊亦/即己壬)
又戊壬为己壬(即丙戊亦/即戊癸)之四倍则戊壬股幂内有己
壬句幂四合之为戊己弦幂则戊己幂内有己壬幂五

矣
而丙己弦幂内复兼有戊己股幂及丙戊句幂是丙己
幂内有丙戊幂六也丙己既同圆径则取其幂六之一
开方必丙戊容方边矣
立方内容十二等面其内又容立方(此相容/比例)
　　　　　　　　　　立圆内容十二等面其内又
　　　　　　　　　　容立方此立方之面幂为外
　　　　　　　　　　圆径上面幂三之一而立方

之各角即同十二等面角以切于立圆之面
法以外切浑圆径上幂取三之一为十二等面内小立
方幂平方开之得小立方根根乘幂见积
又简法以十二等面之面幂求其横剖之大线此线即
　　　　　　　　　　十二等面内容小方之边
　　　　　　　　　　如图作甲乙线剖一面为二
　　　　　　　　　　此线在面中最大即为内小
　　　　　　　　　　立方根以此自乘而三之即

小立方外切浑圆径幂
凡立方内容二十等面二十等面内又容浑圆圆内又
容小立方此小立方之各角能同浑圆之切点以切于
二十等面之平面心
　　　　　　　　　　法以内容浑圆径之幂取三
　　　　　　　　　　之一为内小立方之幂平方
　　　　　　　　　　开之得切点相距即小立方
　　　　　　　　　　根以根乘幂见积

简法取内容浑圆之内小立方边求其理分中末之大
分为内容十二等面边
又简法如前求得二十等面内容十二等面之一面乃
求其横剖之大线即二十等面内容小立方之根　以
根自乘而三之即二十等面内容浑圆之径幂　开方
得根即内容浑圆径　折半为分体之中高
　　　　　　　　　　此二十等面之面作三分之
　　　　　　　　　　一横剖

　　　　　　　　　　此十二等面之面在二十等
　　　　　　　　　　面内
　　　　　　　　　　此五等面边即前横线所成
　
凡五等边平面其边即七十二度之通弦横剖大线即
一百四十四度之通弦各折半为正弦可以径求
一率　　三十六度正弦
二率　　七十二度正弦

三率　　五等边之一边
四率　　横剖之大线
凡十二等面体与二十等面体可互相容而不穷
十二等面体有二十尖二十等面体有十二尖其各尖
之相距必均其互相容也皆能以其在内之尖切在外
各面之中心而遍
凡二十等面内容立圆仍可以容二十等面
二十等面内容立圆仍可以容十二等面

　　　　　　　　　　甲心乙　乙心丙　丙心丁
　　　　　　　　　　丁心戊　戊心甲　皆二十
　　　　　　　　　　等面之一面其各三边皆等
　　　　　　　　　　各以庚辛壬癸己为其面之
心若内容十二等面体则十二等面之各尖必切于庚
辛壬癸己等心点
今求内容十二等面之边则必以庚辛等心点联为直
线即成五等边面之边而与十二等面之形相似而可

　　　　　　　　　　以相容矣
　　　　　　　　　　法当以边(如甲/戊)半之(如甲/辰)作
　　　　　　　　　　对心垂线(如辰/心)成心辰甲句
股形既得己卯倍之为己庚即内容十二等面之一边
二十等面体内容十二等面之图
　　　　　　　　　　第一图原形如五面扁锥心
　　　　　　　　　　尖锐起甲心戊等三等边平
　　　　　　　　　　面凡五共辏而成一心尖乃

二十等面四之一
其己庚辛壬癸五点皆三等边平面之中心亦即内容
十二等面之棱尖所切故必先求此点
简法曰以甲戊边半之于辰作辰心对角斜垂线又以
心甲心戊各取三分之二为心子心丑乃联子丑为线
与甲戊边平行与辰心垂线十字交于己点则己点即
甲心戊平面之心再从子至午作与边平行线线之半
即庚点馀三面尽如此作平行线则辛点在午未线壬点

在未酉线癸点在酉丑线但半之皆得心矣
第二图剖形是五等边平面
　　　　　　　　　　因前图所作子丑等平行线
　　　　　　　　　　横剖之去其中高之尖成子
　　　　　　　　　　午未酉丑五等边平面此平
　　　　　　　　　　面之心点在前图心顶之内
惟子丑等边线是原形所作平行线在体外可见馀皆
以剖而成乃从各角作线至心如子心等分形为五皆

平面三角形而心子等线皆小于子丑边因子己原边
及子心丑角求得心己垂线及子心对角线
第三图正用之形即内容十二等面之一面
　　　　　　　　　　因前第二图各平分其边得
　　　　　　　　　　己庚辛壬癸五点即原形之
　　　　　　　　　　平面心又联此点作己庚等
直线则成此形以此形为内容十二等面之一面则己
庚等五点为十二等面之锐角而皆切二十等面之平

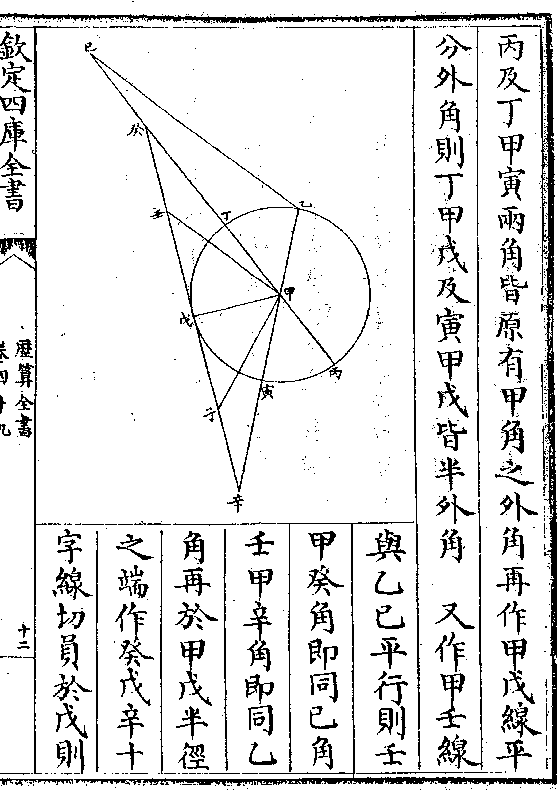面心矣
求己庚线法因心子对角线及心己垂线子己原半边
得己卯倍之为己庚
第一图
设二十等面边一百　甲戊等五边甲心等五辏顶线
并同　则子心六十六(六/六)　子丑平行线同　皆为原
边三之二　心己斜垂线五十七(七三/五○)　为心辰斜垂
线三之二

以上用第一图乃斜立面也
第二图
子己半边三十三(三/三)　子心对角线五十六(七○/九九)
己心垂线四十五(八七/九二)
法为全数与五十四度之割线(一七○/一三○)若子己边与子
心也子己乘割线以全数十万而一得子心
又全数与五十四之切线(一三七/六三八)若子己边与己心也
子己乘切线以全数十万而一得己心　凡全数除降

五位
第三图　仍从第二图生
己庚等两平面心相距线五十三(五八/一六)　其半己卯二
十六(七九/○八)
法为子心对角线与己子半边若己垂线与己卯也
倍己卯得己庚
求得二十等面边一百　内容十二等面其边五十三
(五八/一六)

捷法但用法联两平面之中心点即为内容十二等面
之边　两平面心相联为直线之图
　　　　　　　　　　乙心甲及戊心甲两等边平
　　　　　　　　　　三角面以甲心边为同用之
　　　　　　　　　　边而甲心隆起如屋之山脊
　　　　　　　　　　两平面之中心为己为庚联
　　　　　　　　　　为己庚线与甲心为十字然
　　　　　　　　　　不𦂳相切何也甲心既隆起

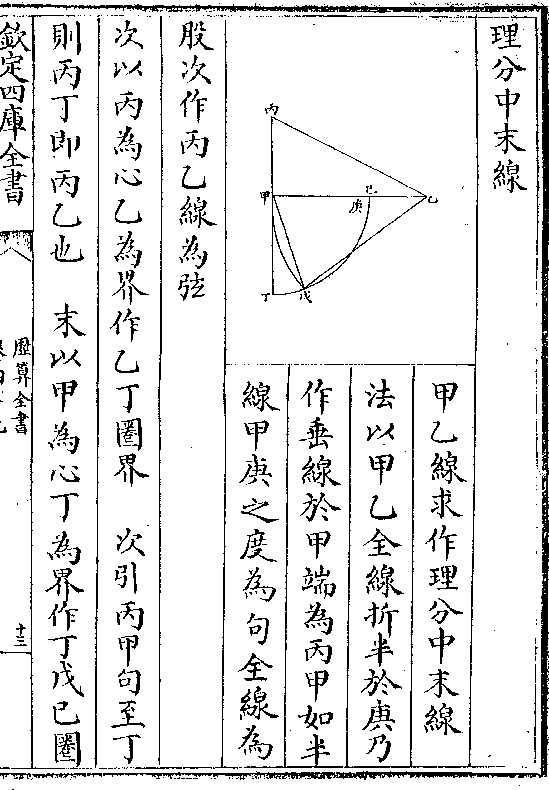　　　　　　　　　　则甲心折半之卯在己庚折
　　　　　　　　　　半之柳点上其距为卯柳
　　　　　　　　　　试侧视之则甲心戊面变为
　　　　　　　　　　戊卯线甲心乙面变为卯乙
　　　　　　　　　　线而甲卯心线变为卯点己
　　　　　　　　　　庚点在平面原近甲心点为
卯戊卯乙三之一则卯柳之距亦为垂线三之一矣
二十等面从腰横剖之图

　　　　　　　　　　凡二十等面体其面之边皆
　　　　　　　　　　等而皆斜交故边皆高于面
　　　　　　　　　　面之中心如己如庚是距体
　　　　　　　　　　心最近之处故为内容浑圆
及十二等面所切之点也
边之两端又高于其折半之处边所辏为尖如甲如戊
如乙如心等是距体心最远之处故为外切浑圆及外
切十二等面之尖也　其各边折半之点如寅如卯其

距体心在近远酌中为外切立方之半径其内切之己
庚外切之甲戊乙心等赖寅卯距心之线为用然后可
知故其用最要
横剖所成之面(十二等面从腰/横剖其根亦同)
　　　　　　　　　　问各边既高于面而又斜交
　　　　　　　　　　何以能横切成平面乎曰从
　　　　　　　　　　右图观之甲戊尖最高则其
　　　　　　　　　　所对之乙心等边似平矣而

乙心等尖亦高则其所对之甲戊等边又平一高一平
彼此相制而成相等之距故寅卯等折半之处其距体
心皆等联之为线即成相等之线而皆平行也
然则何以知其为十等边平面曰准右图上下各五面
其腰围亦上下各五面而尖牙相错成十面今各从其
半边剖之则必为十边平面无疑也
如图奎卯寅十等边平面以中为心
　　　　　　　　　　中寅中卯皆原体心与其边

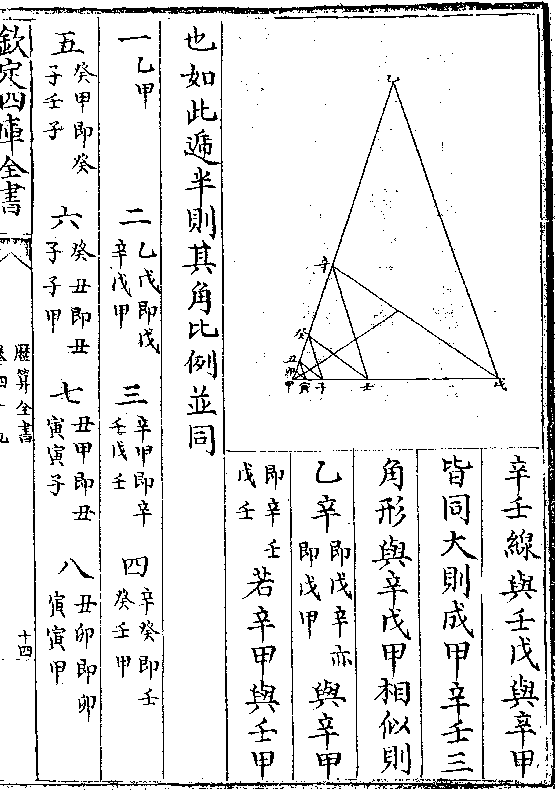　　　　　　　　　　折中处相距之半径亦即为
　　　　　　　　　　外切立方之半径也于前图
　　　　　　　　　　作外切之奎角卯寅平图则
寅卯等即为分圆线乃全圈十分之一当三十六度
理分中末线图
　　　　　　　　　　奎中为全径井中为半径以半
　　　　　　　　　　径(设五/十)为句全径(设一/百)为股
　　　　　　　　　　求其弦得一百一十一(八○/三三)

(九/八)为井奎　以井为心中为界作圆分如中斗截井奎
线于斗则井斗亦半径也　以井斗减井奎其馀斗奎
即为理分中末线之大分(亦即/奎牛)　以奎牛为度作点于
倍径之圈周而遍即成十平分圈周之点联其点为线
即成寅卯等十等边故十等边之寅卯等即木圈半径
之理分中末大分也　若奎中为半径则井中为半半
径亦同
奎中全数(半/径)设一百　寅卯必六十一(八○三/三九八)即半径

理分中末之大分(奎牛即/奎斗)
理分中末线　法以全数一百之幂一万为股幂其半
五十之幂二千五百为句幂并得一万二千五百为弦
幂开方求其根得一百一十一(八○三/三九八)以半数五十减
之得六十一(八○三/三九八)为理分中末之大分即三十六度
之分圆线也
半之为十八度之正弦三○九○一六九九(八线表作二/三○九○)
二十等面分体之图

　　　　　　　　　　甲戊心为二十等面之一面
　　　　　　　　　　其三边等中为体心
　　　　　　　　　　甲中戊中心中皆各面之锐
　　　　　　　　　　角距体心之线又为体外切
　　　　　　　　　　浑圆及外切十二等面之半
　　　　　　　　　　径
　　　　　　　　　　以甲戊心面为底依甲中戊
　　　　　　　　　　中心中三线剖至体心中成

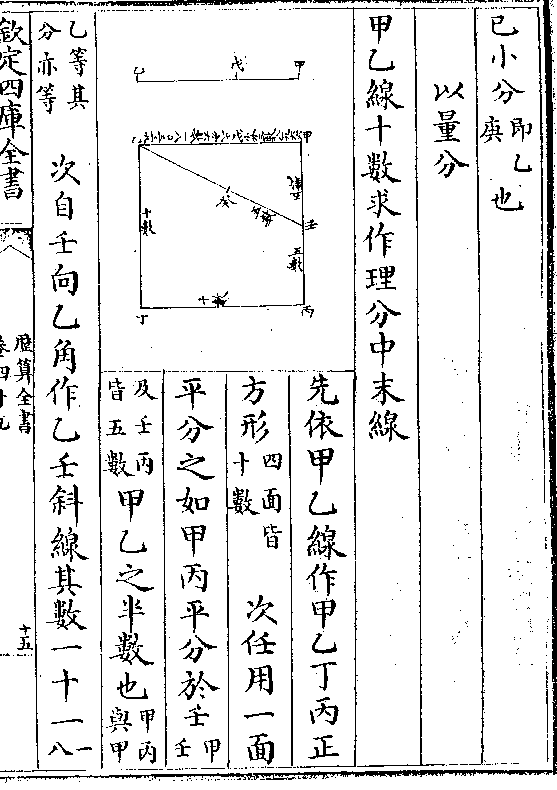　　　　　　　　　　三角锥体为二十等面体二
　　　　　　　　　　十之一
　　　　　　　　　　锥体之底各以其三边半之
　　　　　　　　　　于寅于辰于卯从此三点作
线而体心之中点皆为锥体各立面之斜垂线如辰中
即为甲中戊立面之斜垂线寅中为甲中心立面之斜
垂线卯中为戊中心立面之斜垂线并同
又联寅卯辰三点为寅卯卯辰辰寅三线成寅卯辰小

等边平三角面以此为底依寅中卯中辰中三斜垂线
剖至体心之中点成小三角锥体其积为大三角锥四
之一其寅卯等边为原边二之一　原设边一百则寅
卯五十
其己点为三角面之中心(大小/并同)　己中即分体之中高
(大小锥/体同)是即内容浑圆之半径亦即内容十二等面体
各尖距其体中心之半径
其辰中卯寅中卯卯中辰皆立三角面皆为横剖成十等

边平面之分形故寅卯与寅中之比例若理分中末线
之大分与其全数也
今求寅中线(即外切立方半/径卯中亦同)
一率　理分中末之大分　　　　　六十一(八○三/三九八)
二率　全数　　　　　　　　　　一百
三率　寅卯(剖形十等边之/一即原边之半)　　　　五十
四率　寅中　　　　　　　　　　八十○(九○/一七)
　按寅中线为量体之主线既得此线即可以知馀线

　而此线实生于理分中末线几何原本谓分中末线
　为用最广盖谓此也
次求己中(即内容浑圆及十/二等面之半径)
　　　　　　　　　　甲戊原边设一百半之于寅
　　　　　　　　　　作寅己垂线至己心(乃平/面心)
　　　　　　　　　　己寅二十八(八六/七五)为句其幂
　　　　　　　　　　八百三十三(三三/三三)　用捷法
　　　　　　　　　　以边幂一万取十二之一得

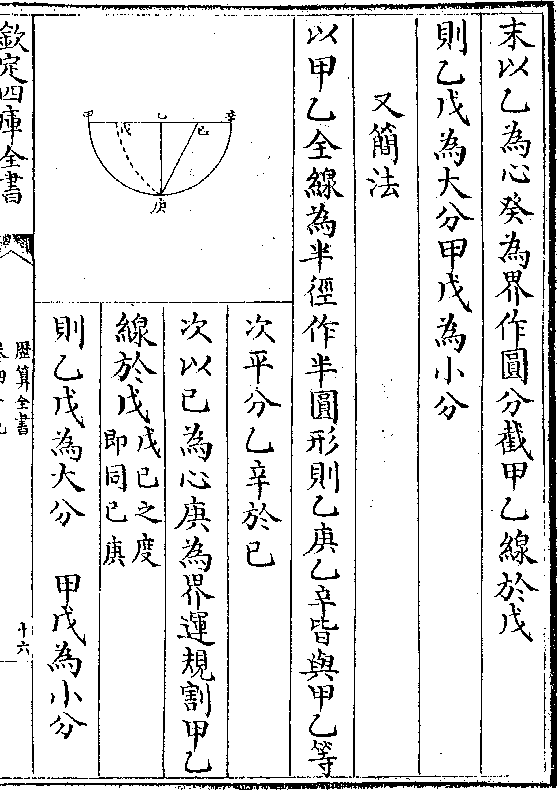　　　　　　　　　　之
　　　　　　　　　　寅中八十○(九○/一七)为弦其幂
　　　　　　　　　　六千五百四十五(○八/五○)
　　　　　　　　　　句幂减弦幂馀五千七百一
　　　　　　　　　　十一(七五/一七)开方得股为己中
　　　　　　　　　　七十五(五七/六一)
订定寅中线
一率　理分中未线大分　六十一(八○三/三九八)

二率　全数　　　　　　一百
三率　寅卯(剖形十等边之/一即原边之半)五十
四率　寅中(即外切立/方之半径)　　八十○(九○/一七)
订定己中线
甲戊边原设一百(半之于寅/作寅己线)
己寅句二十八(八六/七五)　幂八百三十三(三三/三三)
寅中弦八十○(九○/一七)　幂六千五百四十五(○八/五○)
己中股幂五千七百一十一(七五/一七)　根七十五(五七/六一)

末求己庚线(两平面心相联即内/容十二等面之边)
一率　寅中八十○(九○/一七)　为大弦
二率　己中七十五(五七/六一)　为大股
三率　寅己二十八(八六/七五)　为小弦
四率　己星二十六(九六/七二)　为小股
倍己星得五十三(九三/四四)为己庚
解曰中寅己大句股形与己寅星小句股形同用寅角
则其比例等而为相似之形故也

　己庚等线相联成五等边平面图
　　　　　　　　　　准前论甲心戊等三角平面
　　　　　　　　　　合二十面为二十等面体则
　　　　　　　　　　甲心等边线皆高于平面而边
　　　　　　　　　　线之端五相辏即为尖角(如/心)
　　　　　　　　　　(点/)依此推知甲乙丙丁戊点
皆必与他线五相辏而成尖角矣
其己庚辛壬癸各点为各平面之最中央在体为最平

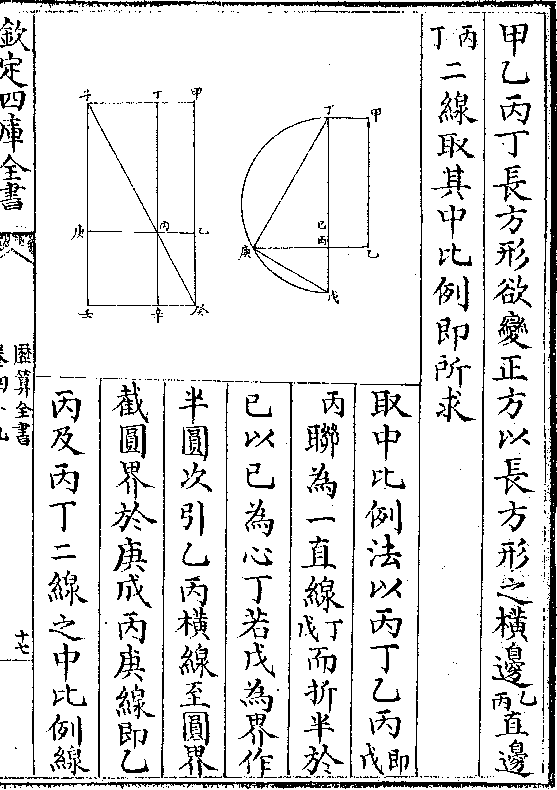之处故内容之浑圆及内容之十二等面各尖必切此
点
今依前法求得己庚等点相联为直线则凡五平面相
辏为尖必有各中央之点相联为线而皆成五等边平
面形矣(此平面形正/与心尖相应)　依此推知甲乙丙丁戊各点皆
能为尖则其周围相辏之五平面亦必各以其中央之
点相联为线而皆成五等边平面形　二十等面体以
五边线相辏之尖凡十有二每一尖之周围皆有五平

面即皆有中央之点相联而成五等边平面亦十有二
　如此而内容十二等平面体己成故曰但联己庚二
点为线即内容十二等面之边也
　求甲中线(即外切浑圆及十二等面/之半径心中戊中并同)
　　　　　　　　　　寅甲为原边之半设五十其
　　　　　　　　　　幂二千五百为句幂
　　　　　　　　　　寅中为外切立方半径八十
　　　　　　　　　　○(九○/一七)其幂六千五百四十

五(○八/五○)为股幂并句股幂九千○四十五(○八/五○)平方开
之得甲中弦
依法求得甲中九十五(一○/六五)
求体积
设边一百其半五十　斜垂线八十六(六○/二五)　相乘得
面幂四千三百三十○(一二/五○)
又以己中高七十五(五七/六一)乘面幂得柱积三十二万七
千二百五十三(九六/○○)

三除之得分体积一十○万九千○八十四(六五/○○)
以二十乘之得全积二百一十八万一千六百九十三
十二等面分体之图
戊辛庚己壬五等边形即十二等面立体之一面　亦
即分体形之底(乃五面立/锥形之底)丙为平面心
丙丁为平面心至体心之垂线亦即分体形之中高又
为体内切浑圆之半径亦即为内切二十等面之半径
丁为全体之中心又为十二分体之上锐即五等面立

锥形之顶
戊辛壬庚等皆各面之外周线(即边/也)为体之棱亦名之
　　　　　　　　　　为根
　　　　　　　　　　自分面之心丙作垂线至边
　　　　　　　　　　(如癸丙/甲丙)分各边为两其分处
　　　　　　　　　　为癸为甲(即各边/折半处)
乃自癸至甲联为癸乙甲线又自此线向丁心平剖之
成甲丁癸三角形面各分形俱如此切之成十等边平

面形故丁癸丁甲皆分体形自顶锐至各边之斜垂线
在所切之十等边平面形即为自丁心至平面角之线
(甲癸等点在各边为折中/在切形之平面则对角)
又自丁至体周各角之线(如丁辛丁/庚丁戊等)在分体即为自底
角至顶锐之棱又为外切浑圆之半径又为外切二十
等面之半径
　先算十二等面之面(即戊辛/庚己壬)
法为全数与五十四度之切线若甲辛与甲丙也　以

甲丙乘甲辛又五乘之得戊辛庚己壬五角面积(甲丙/辛角)
(为五等边之半角三十六度/其馀角甲辛丙必五十四度)
　次算面上大横线(即甲/癸)
又全数三十六度之正弦若甲丙与甲乙也倍甲乙得
甲癸
　次算中高线(丙/丁)
法为全数与七十二度之割线若甲乙与甲丁也(因平/切十)
(等边为三十六度半之为十八度/其馀角七十二度即乙甲丁角)

乃以甲丁为弦甲丙为句两幂相减开方得股即丙丁
也
　次算分体之积
法以中高丙丁乘戊辛庚己壬底而取其三之一为分
形积
　末以十二为法乘分形积得总积
简法以分形中高乘底又四乘之即得总积(三归三因/对过省用)
　算甲丙

一率　全数　　　　　一○○○○○
二率　五十四度切线　一三七六三八(相乘得六八/)
三率　设根之半(甲辛/)　　　　　五○(八一九○○/)
四率　甲丙　　　　　六八　(以全数除之减/五位为畸零)
　算甲乙
法为全数与三十六度之正弦若甲丙与甲乙也
一率　全数　　　　　一○○○○○
二率　三十六度正弦　○五八七七九

三率　甲丙　　　　　六八八一九○
四率　甲乙　　　　　四○四五一一
　　　　　　　　　　甲癸为横切十等边平面之一
　　　　　　　　　　其半为甲乙丁即总形之心
　　　　　　　　　　亦横切平面之心
　算甲丁
法为全数与十八度之馀割若甲乙与甲丁也
一率　全数　　　　　一○○○○○

二率　七十二度割线　三二三六○七
三率　甲乙　　　　　四○四五一一
四率　甲丁　　　　　一三○九○二五
　算丙丁中高线
法以甲丁为弦　甲丙为句　求得股为丙丁
算得丙丁一百一十一(三五/二六)为中高线亦即十二等面
形内浑圆之半径
　算五等边面幂

法以甲丙乘甲辛五十得三千四百四十○九半又五
乘之得一万七千二百○四七五为五等边(边各/一百)之平
幂亦即十二等面分形之底积
　算总积
用简法以底积一七二○四七五四因之得六八九九
○以乘中高得七百六十八万二千二百一十五八七
四○为十二等面之积
　计开十二等面

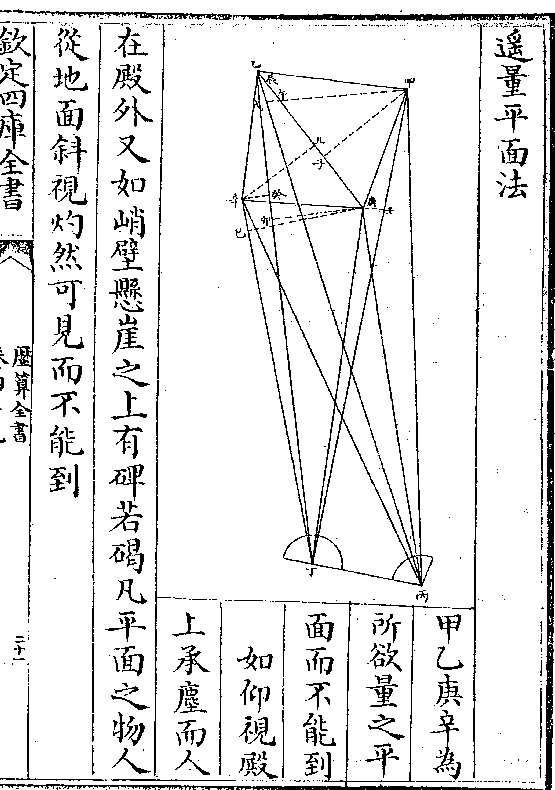一率　七六八二二一五　　例容
二率　一○○○○○○　　例边上立积
三率　一○○○○○○　　设容
四率　○一三○一七○　　求得设边上立积
立方法开之得其根五十
　与比例规解合与测量全义差四千一百七十四为
　二百分之一
　算辛丁(庚丁戊/丁并用)　又即为外切浑圆半径

法以甲丁股幂(一七一/三五)甲辛句幂(○二五/○○)并为弦幂(一/九)
(六三/五)求得弦数一百四十○为辛丁即外切圆半径
　计开
十二等面之数
设边一百　其容积七百六十八万二二一五
内容浑圆径一百二十二　外切浑圆径二百八十
捷法十二等面边求外切内容之立方及外切之立圆
置十二等面边为理分中末之小分求其大分为内容

立方边内容立方边自乘而三之开方得外切立圆全
径
又置十二等面边为理分中末之小分求其全线为外
切立方边
一率　理分中末之小分(三十八一九/六六○一)　理分中末之大分
二率　理分中末之大分(六十一八○/三三九八)　理分中末之全分
三率　十二等面之边
四率　内容小立方边　即大横线

　又
一率　理分中末之小分
二率　理分中末之全分
三率　十二等面之边
四率　外切立方边
以十二等面边减外切立方边馀为内容立方边
以内容立方边加十二等面边即外切立方边
又捷法但以十二等面边加大横线(即小立/方边)　即外切

立方边
　立方内容十二等面算法　用理分中末线
　　　　　　　　　　　此五等边面为十二等面之
　　　　　　　　　　　一
　　　　　　　　　　　巳为平面心　中为体心
　　　　　　　　　　　寅卯为戌亥大横线之半(三/十)
(○九○一/六九九)卯中寅中为外切立方半径(五/十)　戌亥为面之
大横线(六十一八○/三三九八)为理分中末之大分亦即内容小

立方之根
巳寅巳卯俱平面容圆半径
巳中为内容立圆半径即分体中高
丑中为外切立圆半径(亥中戌/中并同)
设立方根一百为径　半径五十为寅中卯中　理分
中未大分之半为寅卯(三十○九○/一六九九)　又半之为寅子
(一十五四五/○八四九五)为理分中末大分四之一
一率　全数　　　　　　一○○○○○

二率　五十四度之割线　一七○一三○
三率　寅子　　　　　　(一十五四五○/八四九五)
四率　寅巳(即卯/巳)　　　　二六二八六五
　求得卯巳为平面中垂线
一率　全数　　　　　　一○○○○○
二率　三十六度之切线　○七二六五四
三率　卯巳　　　　　　二十六二八六五
四率　卯丑(即半/边)　　　　一十九○九八二

　倍卯丑得丑亥边三十八(一九/六四)即十二等面边乃理
　分中末大分之大分也以此知大横线与五等边为
　理分中末之全分与其大分之比例也
卯巳句幂(○六九/○九八)　卯中弦幂(二五○/○○○)相减为股幂一
八○九○二　开方得巳中(四十二五/三二五)为内容浑圆半
径
卯丑句幂(○三六四七/四一二四三)　卯中股幂(二五/○○)　相并为弦
幂(二八六四七/四一二四三)　开方得丑中(五十三五/二三二)为外切浑圆

半径
丑亥巳卯相乘五因二除为面幂以乘巳中而四因之
得十二等面积
简法
十二等面内容小立方(六十一八○/三三九八)即理分中末之大
分盖戌亥大横线倍大于寅卯故也　大横线即小立
方之边
以大横线之幂三因之开方得亥中为外切浑圆半径

(丑中/同)
又立方根与所容十二等面边若全数与理分中末之
小分
约法
立方根与其所容十二等面体内小立方之根若全数
与理分中末之大分
凡立方外切浑圆则径上幂三倍于方幂
　计开

立方设径一百
内容十二等面边三十八(一九六/六○一)
内容小立方边六十一(八○三/三九八)
外切浑圆径一百○七(○四六/六二五)　即丑中亥中倍数
外切浑圆半径(五十三五/二三三)　即丑中亥中
内容浑圆半径四十二(五三/二五)　即已中　为分体中高
内容浑圆全径八十三(○六五/一)
内容二十等面边四十四(七二/一一)

　几何补编卷三
十二等面体分图　用理分中末线
　
　
　
　
　
辛戌亥五等边形为十二等面之一

寅卯点为边折半处中为体心
卯中为外切立方半径(设五/十)
卯亢为外切立方全径(设一/百)
寅卯线与卯中半径若理分中末之大分与其全数也
在圆内为三十六度之分圆　辛癸辛戌等俱七十二
度之分圆
乙巳为半径(己丑/同)乙癸为三十六度之通弦
乙已半径与乙癸亦若理分中末一之全数与其大分也

故乙已癸三角形与卯中寅相似
若取乙丙切线如乙癸之度则丙巳必同亥癸边(即七/十二)
(度通/弦)折半于甲则甲乙为十八度正弦再于寅卯线取子壬
如乙甲取壬癸如乙己半径引已子至癸中末乃自卯作
线至中与壬癸平行因得寅中与卯中等则寅中卯即
为横切之半面
一率　全数　　　　　一○○○○○
二率　三十六度割线　一二三六○七

三率　子寅　　　　　一十五(四五○八/四九五)
四率　丑寅半边　　　一十九(○九八三/)
倍丑寅得丑戌三十八(一九/六六)与简法合
论曰凡十二等面从其半边之点(如寅/如卯)联为线以剖至
体之心(中/点)则所剖成寅中卯三角形平面必为全圆十
之一即寅中卯角必三十六度而中寅或中卯两弦与
寅卯底若理分中末之全分与其大分矣
又十二等面在立方形内必以卯中(或寅/中)自心至边之

线当立方之半径是立方半径与十二等面之寅卯线亦
若理分中末之全与其大分也　若设立方半径一百则
寅卯必六十一(八○三/三九八)如理分中末之大分也今设立方
全径一百其半径五十则寅卯亦必三十○(九○一/六九九)如大
分之半矣　寅卯二点既在(丑戌/丑亥)两边之折半则戌亥大
横线必倍大于寅卯而与理分中末大分之全相应为六
十一(八○三/三九八)　此皆设立方半径五十之数也而半径五
十其全径必一百故知设径一百则十二等面之大横线

必六十一(八○三/三九八)而竟同理分中末大分之数也
既得此大横线则诸线可以互知
　　　　　　　　　　试先求边　法为酉戌(半大/横线)
　　　　　　　　　　与丑戌等边若全数与三十
　　　　　　　　　　六度之馀割线也
　一率　全数　　　　　一○○○○○
　二率　三十六度割线　一二三六○七
　三率　酉戌半大横线　三十○(九○一/六九九)

四率　丑戌全边　　　三十八(一九/六六)
论曰五等边各自其角作线至心分形为五则各得七
十二度角(如丑巳戌等其巳/角皆七十二度)其半必三十六度(如寅已/丑之巳)
(角得戊已丑之/半正三十六度)而丑戌酉与丑巳寅皆句股又同用丑
角则戌角与巳角等为三十六度
十二等面求积
平面中垂线(卯/己)二十六(二八/六五)
边(即丑亥/丑戌等)三十八一九(六/六)　半边(即丑卯/丑寅)一十九(○九/八三)

一面之平幂二千五百一十○(一三/七○)
内容浑圆半径四十二(四三/二五)　即分体五面立锥之中
高(已/中)　中高三之一一十四(一四/四一)
分积三万五千四百九十五(八四/七三)　其形为五面立锥
其体积为十二之一
全积四十二万五千九百五十○(一六/七六)
外切立方根一百　其积一百万
外切浑圆径一百○七(○四/六六)

内容立方根六十一(八○三/三九八)
外切立方与体内容立方径之比例若理分中末之全
分与其大分
又若外切立方之外又切十二等面体体外又切大立
方则大立方之径与今所算外切立方径亦若理分中
末之全分与其大分而外切之十二等面与其内十二
等面径亦必若理分中末之全分与其大分也
孔林宗云外立方与内立方之径为理分中末线全分

与大分之比例是矣若内立方之内又容立圆则小立
圆之径与小立方之径同而外浑圆与外立方之径不
似未可以前比例齐之
若十二等面外切大立方大立方之外又切大立圆大
立圆外又切十二等面则大立圆与内容小立圆亦必
若理分中末之全分与其大分而外切十二等面与十
二等面亦必若理分中末之全分与其大分何则皆外
切立方与内容立方之比例也

十二等面容二十等面图
　第一图
　　　　　　　　　　割十二等面之三平面一尖
　　　　　　　　　　成此形癸丑丙丑戊丑俱五
　　　　　　　　　　等边平面皆十二等面之一
　　　　　　　　　　(已庚辛各为/其中心一点)
丑为三平面棱所聚之尖　亥丑戌丑乙丑俱平面边
各为两平面所同用之棱　中为体心　巳中辛中庚

中皆内切浑圆半径亦内容二十等面自尖至体心半
径　巳卯庚卯巳寅辛寅辛壬俱平面中垂线　寅卯
壬皆平面边折半之点
　第二图
　　　　　　　　　　内容二十等面体各自其边
　　　　　　　　　　剖至心成此分体为内容体
　　　　　　　　　　二十分之一　辛庚巳三角
　　　　　　　　　　尖即十二等面之中心原点

此点以外俱剖而得甲点与卯点同在卯中线而甲在
卯之下丁在寅下辰在壬下俱同
　第三图
　　　　　　　　　　自卯点起依卯己卯庚二线
　　　　　　　　　　剖至体心中成此平面形卯
　　　　　　　　　　即原边折半处卯中即原体
　　　　　　　　　　外切立方之半径中即体心
已庚即原两平面之中心点今联为(已/庚)线即内容二十

等面之一边
已中庚即内切二十等面分体之立面乃三角锥体之
一面　甲中为内切二十等面分体之斜垂线　观第
二图可明(第二图角点居剖内三角之中心正对原体/之丑尖而在其下故角中为内容分体之正)
(高而甲中为/斜垂线也)
今求已庚线(即内容二十/等面之边)
法于卯中(外切立/方半径)内求甲中以相减得卯甲为股用与
卯已弦(原体之面/上中垂线)两幂相减开方得句为已甲倍之得

巳庚
卯已中三角形
卯中即外切立方半径设五十为底
卯已即原体之平面中垂线二十六(二八/六五)
　　　　　　　　　　巳中即内容浑圆半径亦即
　　　　　　　　　　内容二十等面分体之斜棱四
　　　　　　　　　　十二(五三/二五)
　　　　　　　　　　以卯巳巳中两弦相减为较

相并为总以总乘较为实卯中底五十为法除之得亢
中二十二(三六/○六)以减卯中馀二十七(六三/九四)为亢卯折半
得一十三(八一/九七)为卯甲
　计开
立方根设一百其半五十(即卯/中)亦为十二等面自体心
至边
十二等面之平面中垂线(即卯/巳)二十六(二八/六五)
十二等面内容浑圆半径(即已/中)四十二(五三/二五)亦为内容

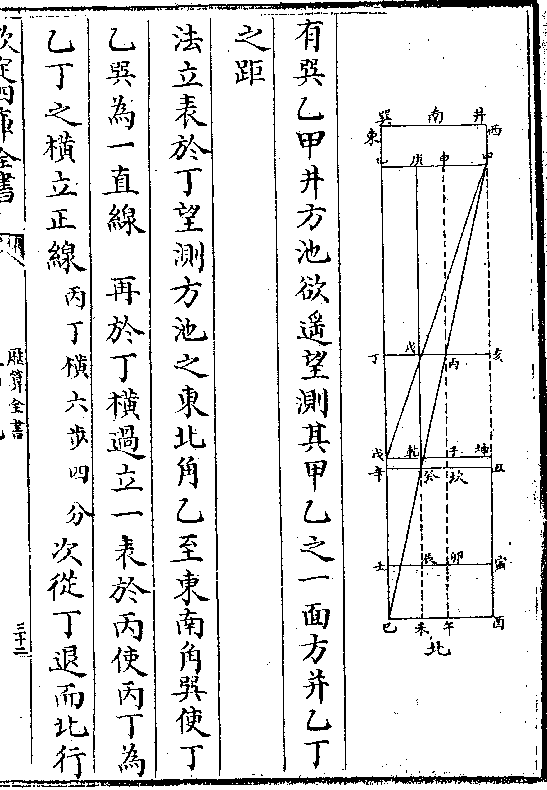二十等面自尖角至体心分体以为锥体之棱
卯巳已中之较一十六(二四/六○)　总六十八(八一/九○)
较总相乘一千一百一十八(○三/三四)为实　卯中五十为
法除之得中亢二十二(三六/○六)　以中亢减卯中五十馀
二十七(六三/九四)为亢卯折半得一十三(八一/九七)为卯甲以卯甲减
卯中馀三十六(一八/○三)为甲中即内容二十等面分体之
斜垂线
卯巳自乘得六百九十○(九八/○○)为弦幂

　　　　　　　　　　卯甲自乘得一百九十○(九/八)
　　　　　　　　　　(四/一)为股幂　相减馀四百九
　　　　　　　　　　十九(九九/五九)为勾幂　开方得
　　　　　　　　　　巳甲二十二(三六/○五)　倍之得
巳庚四十四(七二/一一)即为内容二十等面边
　此法甚确亦且甚捷无可疑者偶于枕上又思得一
　法借灯体分形之三角锥以求十二等面内容二十
　等面分体之三角锥是以锥体相截而知其所截之

　　　　　　　　　　边即为内容二十等面之边
　　　　　　　　　　第一图
　　　　　　　　　　丑为三平面所聚之尖　丑
　　　　　　　　　　戌丑亥丑乙皆两平面同用
　　　　　　　　　　之棱　巳庚辛皆五等边平
面之心　己寅己卯等皆平面心至边垂线　已牛丑
为平面心对角线　寅卯壬皆平面边折半之点　寅
中卯中壬中为体心至边线即外切立方半径　中为

　心
　第二图
　　　　　　　　　　联寅卯卯壬壬寅三线为平
　　　　　　　　　　三角面横剖之又各依寅中
　　　　　　　　　　卯中壬中线剖至体心中则
　　　　　　　　　　成三角锥体二其一为丑寅
卯壬体是三角锥而稍扁者也其一为寅卯壬中体是
三角锥而稍长者也其寅卯壬三角平面为扁形之底

又为长形之面其寅卯等线与寅中卯中之比例皆若
理分中末之大分与其全分也其扁形锥既剖而去则
成圆灯所存长锥即灯形分体之一平面心之点为斗在丑尖
下与牛点平故丑牛为弦则斗牛如勾而丑牛之距如股也
　　　　　　　　　　第三图
　　　　　　　　　　又于圆灯分体剖去辰甲丁
　　　　　　　　　　之一截则成甲丁辰中三角
　　　　　　　　　　锥乃十二等面内容二十等

面分体中之分体其辰甲丁面与巳庚辛吻合为一盖
巳庚辛者内容二十等面之一面各于边折半为甲丁
辰而联之为线则成小三角于中故辰丁等线皆居巳
庚线之半而甲中原为二十等面分体之斜垂线者今
则为三角锥之楞
　　　　　　　　　　第四图
　　　　　　　　　　己牛丑即原平面从心至角
　　　　　　　　　　尖之线丑斗角中即原体自

尖至中心之线又为外切浑圆半径
依第二图截丑巳于牛而横剖之亦截丑中于斗成丑
斗牛勾股形　又依第三图截斗中于角成丑角巳勾
股形此两勾股相似而比例等
法为丑牛与丑斗若丑巳与丑角也
　　　　　　　　　　第五图
　　　　　　　　　　寅中卯三角形为圆灯分体
　　　　　　　　　　之立面截为甲丁中三角形

此两形相似而比例等　法为卯中与卯寅若甲中与
甲丁也
又斗中为圆灯分体之中高其平面为寅卯壬角中为
截体之中高其平面为丁甲辰此两体相似而线之比
例等　法为斗中高与寅卯阔若角中高与甲丁阔
先求丑斗高
用截去扁三角锥以牛卯(即寅卯/之半)自乘幂三分加一以
减丑卯幂为丑斗幂开方得丑斗高

次求丑角高
用巳丑对角线乘丑斗以丑牛除之得丑角高　其丑
牛线以牛卯幂减丑卯幂开方得丑牛　巳寅丑寅两
幂并开方为己丑
末求巳庚线
用丑角减丑中得角中　又用丑斗减丑中得斗中
以角中乘寅卯以斗中除之得甲丁倍甲丁得己庚为
内容二十等面之边

理分中末线　以量代算
　　　　　　　　　　先以巳为心作图而匀分其
　　　　　　　　　　边为五作甲庚乙丙丁五等
　　　　　　　　　　边平面(即十二等/面之一面)
　　　　　　　　　　乙丁为大横线设一百甲庚
等边必六十一(八○三/三九八)为大横线理分中末之大分
若乙丁大横线设六十一(八○三/三九八)则甲庚等边必三十
八(一九/六六)亦为大横线理分中末之大分

设立方一百　内容十二等面边三十八(一九/六六)为理分
中末之小分亦即大分之大分
十二等面内又容小立方其边与十二等面之大横线
等六十一(八○三/三九八)为大立方边一百与十二等面边三
十八(一九/六六)之中率何也大立方一百乘十二等面边三
十八(一九/六六)开方得根即小立方及大横线六十一(八○/三三)
(九/八)
若大横线自乘之幂以十二等面边除之即仍得外立

方根而以外立方根除大横线幂必仍得十二等面之
边矣
求理分中末线捷法　用前图
作五等边平面　求其大横线(乙/丁)　联两角为线即得
之
次以大横线之一端(如/乙)为心其又一端(如/丁)为界作丁戊
圆分乃引五等边与圆分相遇(如引乙丙至戊/与圆分遇于戊)则相遇
处(如/戊)至圆心(如/乙)为全分(即乙戊亦即/乙丁大横线)原边为大分(即乙/丙)

引出馀边为小分(即丙/戊)
又法
作平三角使两角(如戊/如丁)俱倍大于一角(如/乙)末乃破一倍
　　　　　　　　　　角平分之作线至一边(如平/分丁)
　　　　　　　　　　(角为两作丁丙/线至乙戊边)则其斜线即
　　　　　　　　　　为理分中末之大分(即丁/丙也)
解曰倍破角则与小角等(如破丁角为两/皆与乙角等)而乙丙丁形
之乙丁两角同大则(乙丙/丁丙)两弦亦同大而乙丙既为大

分丁丙亦为大分矣准此又破丙角可以递求于无穷
诸体比例
凡诸体之比例有三
一曰同边之比例可以求积
一曰同积之比例可以求边
一曰相容之比例可以互知
内相容之比例亦有三
一曰立圆内容诸体之比例　所容体又容立圆

一曰立方内容诸体之比例　所容体又容立方
一曰诸体自相容之比例(即同径同/高之比例)或或两体互相容
　或数体递相容
等积之比例　比例规解所用今考定
立方积　　　一○○○○○○　其边一百
四等面积　　一○○○○○○　其边二百○四
八等面积　　一○○○○○○　其边一百二十八
十二等面积　一○○○○○○　其边五十

二十等面积　一○○○○○○　其边七十七
方灯
圆灯
　凡方灯依楞剖之纵横斜侧皆六等边平面凡圆灯
　依楞剖之纵横斜侧皆十等边平面故皆有法形体
等边之比例　测量全义所用今考定
立方边　　一○○　　　　积一○○○○○○
方灯体边　○七○七一○六积○八三三三三三

　　　边　一○○　　　　　积二三五七○二一
八等面边　○七○七一○六　积○一六六六六六
　　　边　一○○　　　　　积○四七一四○四
四等面边　一○○　　　　　积○一一七八五一
十二等面边一○○　　　　　积七六八二二一五
二十等面边一○○　　　　　积二一八一八二二
圆灯体边　○三○九○一七　积○二九○九二九
　　　边　一○○　　　　　积○九八五九一六

等径之比例　　　皆立方所容
立方径　　　　一○○积一○○○○○○　边(一○○/)
内容方灯径　　一○○积○八三三三三三　边(○七○七/一○六)
内容四等面径　一○○积○三三三三三三　边(一四一四/二一三)
内容八等面径　一○○积○一六六六六六　边(○七○七/一○六)
内容立圆径　　一○○积○五二三八○九
内容二十等面径一○○积○五一五二二六　边(○六一八/○三四)
内容十二等面径一○○积○四二五九五○　边(○三八一/九六六)

内容圆灯径　一○○积○二九○九二九　边(○三○九/○一七)
　右以立方为主而求诸体
内立方及灯体之径为自面至面
四等面十二等面二十等面之径皆自边至边(以边折/半处作)
(垂线至对边折半处形如工字四/等面则上下边遥相午错如十字)
八等面之径为自尖至尖　然皆以其径之两端正切
于立方方面之中心一点立方面其相切亦必六点
求积约法

凡立方内容诸体皆与立方之六面同高同阔　则灯
形积为立方积六之五　四等面积为立方积三之一
　八等面积为立方积六之一　以上三者皆方斜比
例
灯形及八等面皆以方求斜法以边自乘倍之开方得
外切立方径以径再自乘得立方积取六之五为灯六
之一为八等面积
四等面则以方求其半斜法以边自乘半之开方得外

切立方径以径再自乘为立方积取三之一为四等面
积
立圆在立方内则其积为立方积二十一之十一
　谨按方圆比例祖率圆径一百一十三圆周三百五
　十五见郑世子律学新说较径七周二十二之率为
　密又今推平圆居平方四百五十二分之三百五十
　五较十四分之十一为密又推得立圆居立方六百
　七十八分之三百五十五较二十一分之十一为密

准立方比例以求各体自相比　皆以同高同阔同为
立方所容者较其积
灯内容同高之八等面　为八等面得灯积五之一
又立圆内容同高之八等面　为八等面得圆积六十
六之二十一(即二十/二之七)　二者皆同高而又能相容
　用课分法母互乘子得之

　准此而知立圆内容八等面其积之比例若围与径
　也
又立方内容十二等面其内又容八等面　又立方内
容二十等面其内又容八等面　二者亦同高而能相
容
同高之四等面积为灯积五之二(即十之四四以灯面四/因退位得 等面积)
同高之八等面积为四等面积二之一
同高之四等面积为立圆积十一之七

　
　
　此三者但以同高同为立方所容而不能自相容若
　相容则不同高
凡立方之灯形内又容立方则内小立方边与径得外
立方三之二体积为二十七之八面幂为九之四
凡灯容立方以其边为方而求其斜为外切之立方边
取方斜三之二为内立方边

立方边一○○　　　　　　面幂一○○○○　　　体积(一○○○/○○○)
灯边　　○七○七一○六　面幂○五○○　　　　体积(○八三三/三三三)
小立方边○六六六六六六　面幂○四四四四四四　体积(○二九六/二九六)
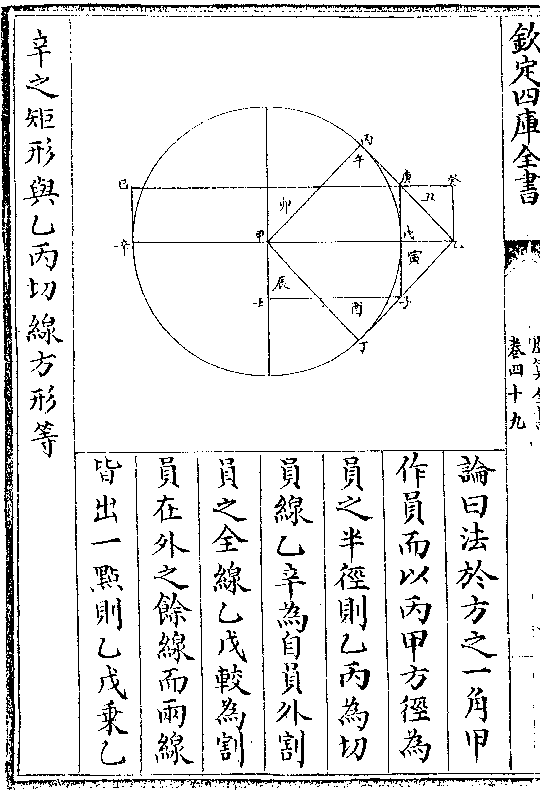
凡方内容圆圆内又容方则内小方之幂得大方三之一
捷法以小方根倍之为等边三角形之边而求其中垂
线即外切立圆之径亦即为外大方之边
如图三边既等则乙丙得甲丙之半若乙丙一其幂亦一而
甲丙二其幂则四以乙丙句幂一减甲丙弦幂四所馀

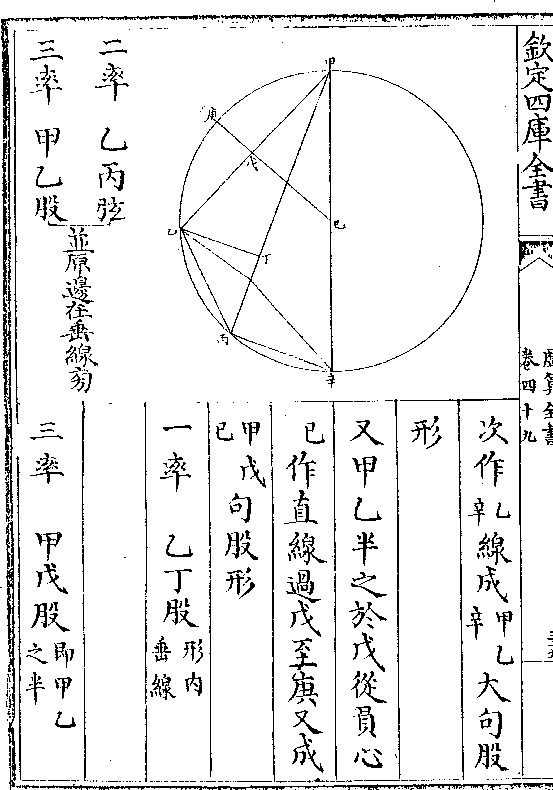　　　　　　　　　　为甲乙股幂三
　　　　　　　　　　内方之幂一而外切浑圆之
　　　　　　　　　　幂三故其根亦如乙丙与甲
乙也　或以小立方之根为句倍根为弦求其股为外
切浑圆径亦同(浑圆径即/外方边)
若以量代算则三角形便
如以大方求小方者则以大方为中垂线而作等边三
角形其半边即小方根也

或用大方为股而作句股形使其句为弦之半即得之
捷法句股形使甲角半于丙角则弦倍于句而句与股
如小立方根与大方根
或以甲角作三十度而自乙作垂线引之与甲丙弦线
遇于丙则乙丙即圆所容方之根
　又按先有大方求小方者取大方根倍之为等边三
　角形之边而求其中垂线以三归之即得
凡立方内容方灯灯内又容立圆圆内又容圆灯灯内

又容八等面凡四重在内其外切于立方也皆同点(切/立)
(方有六处所同者皆在其方面之最中一点若从此一/点刺一针则五层悉透内惟方灯以面切面不可言点)
(若言点则有十二皆/切在立方边折半处)
凡立方内容方灯灯内又容十二等面体体内又容圆
灯灯内又容八等面凡四重在内其切于立方也皆同
处(凡六处皆在立方面内方灯体以面切面十二等/面以边切馀皆以尖切尖切者皆每面之最中点)
凡立方内容方灯灯内又容二十等面体体内又容圆
灯灯内又容八等面同上

凡立方方灯立圆十二等面二十等面圆灯内所容之
八等面皆同大
凡立方内容四等面体体内又容八等面其切立方皆
同处(四等面以边切为立方六面之斜八等面以/尖切居立方各面中心即四等面边折半处)
准此而知立方内所容之八等面与四等面所容之八
等面亦同大且同高各体中所容八等面皆同大因此
可知
凡立圆内容十二等面体　又容立方其立方之角同

十二等面之尖而切于立圆故立圆内所容之立方与
十二等面内所容之立方同大
凡二十等面体内容立圆　内又容立方立方之角切
立圆以切二十等面之面故立圆所容之立方与二十
等面内所容之立方必同大
凡二十等面体内容立圆　内又容十二等面体体内
又容立方此立方之角切十二等面之角以切立圆而切
于二十等面之面皆同处

凡诸体能相容者其相容之中间皆可容立圆此立圆
为外体之内切圆亦为内体之外切圆
惟八等面外切二十等面十二等面四等面及圆灯其
中间难著立圆何也八等面之切圆灯以尖切尖而其
切四等面十二等面二十等面则以尖切边故其中间
不能容立圆
其他相切之中间能容立圆者皆以内之尖切外之面
凡诸体在立方内即不能外切他体惟四等面在立方

内能以其角同立方之角切他体故诸体所容四等面
之边皆与其所容立方之面为斜线
凡诸体相容其在内之体为所容其在外之体为能容
能容与所容两体之相切必皆有一定之处
凡相容两体之相切或以尖或以边(即体/之棱)或以面
浑圆在立方内为以面切面其相切处只一点皆在立
方每面之中央(立方六面相/切凡六点)
立方在浑圆内为以尖切面(立方之角有八/故相切有八点)有一点不

相切者即非正相容也
浑圆在诸种体内皆与在立方内同谓其皆以面切诸
体之面而切处亦皆一点也然其数不同如四等面则
切点有四方灯则切点有六八等面则切点有八十二
等面及圆灯则切点有十二二十等面则切点有二十
其切点之数皆如其面之数而皆在其面之中央也方
灯则以其方面为数圆灯则以其五等边之面为数而
不论三角之面者何也三角之面距体心远故不能内

切立圆也
诸体在浑圆内皆与立方在浑圆内同谓其皆以各体
之尖切浑圆之面也其数亦各不同如四等面则切点
亦四方灯则切点十二八等面则切点六十二等面则
切点二十二十等面则切点十二圆灯则切点三十皆
如其尖之数也
四等面在立方内以边棱切立方之面四等面有六棱
以切立方之六面皆遍其四尖又皆切于立方之角

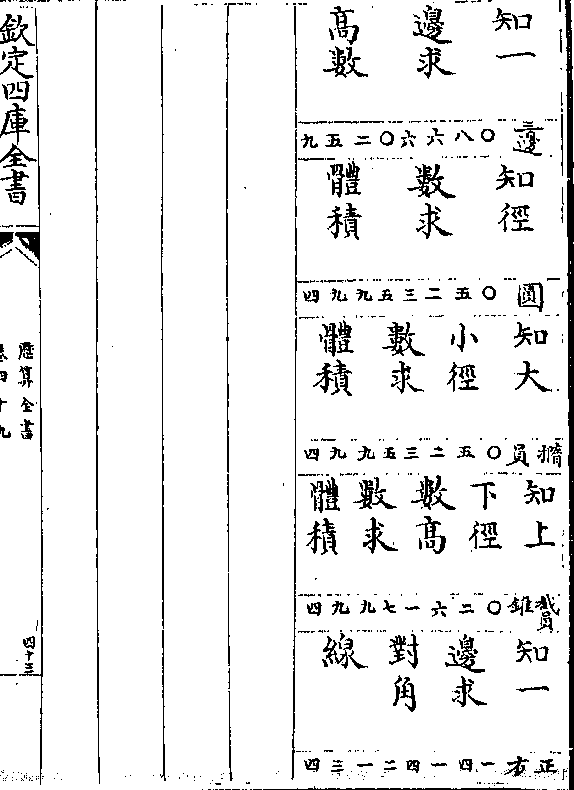十二等面二十等面在立方内皆以其边棱切立方之
面两种各有三十棱其切立方只有其六以立方只有
六面也
　此三者为以楞切面
八等面在立方内以尖切面凡六点　圆灯在立方内
亦以尖切面有六点皆在立方面中尖与八等面同
方灯在立方内则以面切面皆方面也方灯之方面六
亦与立方等也其十二尖又皆切于立方之十二边楞

皆在其折半处为点
十二等面与二十等面递相容皆以内体之尖切外体
之面
十二等面在八等面内以其尖切八等面之面体有二
十尖只用其八也
方灯在八等面内亦以面切面而皆三角面方灯之三
角面有八数相等也又其尖皆切于八等面各棱之中
央折半处棱有十二与灯之尖正等也

圆灯在十二等面内以面切面皆五等边平面也圆灯
体之五等边平面原有十二故也又皆以其尖切十二
等面之边楞而皆在其中半
圆灯在二十等面内亦以面切面皆三角平面也圆灯
体之三角平面原有二十故也又皆以其尖切二十等
面之边楞而皆在其中半
问十二等面与二十等面体势不同而圆灯之尖皆能
切其楞边何也曰圆灯有三十尖而两等面体皆有三

十楞故也
凡能容之体皆可改为所容之体递相容者亦可递改
如立方容圆即可刓方为圆浑圆容方即可削圆为方
递相容者如立方内容浑圆圆内又容十二等面体体
内又容二十等面即可递改
凡所容之体皆可补为能容之体皆以数求之
如立方外切立圆以其尖角则求立方心至角之线为
立圆半径

凡以面切面者其情相通
如方灯以其方面切立方面又能以其三角切八等边
面则此三者皆方斜之比例也
又如圆灯以其五等边面切十二等面又能以其三角
面切二十等面则此三者皆理分中末之比例也
若反用之而令立方在方灯之内则立方之尖所切者必三
角面若八等面在方灯之内则其尖所切又必方面也
若令十二等面在圆灯内则所切者必三角面而二十

等面居圆灯内所切者又必五等边面也故曰其情相
通
诸体相容
凡立圆立方皆可以容诸体
凡立圆内容立方立方内又可容立圆两者不杂他体
可以相生而不穷
凡立圆内容立方此立方内又可容四等面四等面又
可容立圆三者以序进亦可以不穷

凡立圆内容立方又容四等面四等面在立方内以其
尖切立圆与立方尖所切必同点
凡立圆容四等面在立圆所容立方内必以其楞为立
方面之斜依此斜线衡转成圆柱形必为立圆之所容
而此柱形又能含立方
　　　　　　　　　　外圆者柱之底若面内方者
　　　　　　　　　　立方之底若面直而斜者四
　　　　　　　　　　等面之边

凡四等面体在立圆内任以一尖为顶以所对之面为
㡳旋而作圆锥此锥体必为立圆之所容而不能为立
方之容
此两体虽非正相容体然皆有法之体
凡立方内可容八等面八等面又可容立方而相与为
不穷
凡立方有六等面八尖八等面有八等面六尖故二者
相容则所容体之尖皆切于为所容大体之面之中央

而等
凡立方内容立圆此立圆内仍容八等面其八等面尖
切立圆之点即可为切立方之点
八等面内容立圆此立圆内仍容立方则立方尖切立
圆之点亦即可为其切八等面之点
凡立圆可为诸等面体所容其在诸体内必以圆面一
点切诸体之各面此一点皆在其各等面之中心而等
而遍

凡八等面内容立圆仍容立方　立方内仍容四等面
而四等面以其角切立方角即可同立方角切立圆以
切八等面叠串四体皆一点相切必在八等面各面之
中心
立方设一百内容二十等面边六十一(八○三/三九八)内又容
立圆也十三(四一/七二)
简法取内容立圆径幂三之一开方得内容小立方再
以小立方为理分中末之全分而求其大分得内容十

二等面边
凡十二等面二十等面皆能为立圆之所容皆以其尖
切浑圆凡十二等面二十等面皆能容立圆皆以各面
之中心一点正与浑圆相切
凡十二等面与二十等面可以互相容皆以内体之尖
切外体之各面中心一点
凡十二等面内容浑圆浑圆内又容二十等面与无浑
圆者同径二十等面内容浑圆浑圆内又容十二等面亦

与无浑圆同径何也浑圆在各体内皆以其体切于外
体各面之中心点而此点即各内体切浑圆之点故也
以上皆可以迭串相生而不穷
凡十二等面内容浑圆浑圆内又容十二等面亦可以
相生不穷
二十等面与浑圆递相容亦同
凡立方内容十二等面皆以十二等面之边正切于立
方各面之正中凡六皆遥相对如十字

　　　　　　　　　　假如上下两面所切十二等
　　　　　　　　　　面之边横则前后两面所切
　　　　　　　　　　之边必纵而左右两面所切
　　　　　　　　　　之边又横若引其边为周线
　　　　　　　　　　则六处相交皆成十字
　　　　　　　　　　立方内容二十等面边亦同
　　　　　　　　　　凡各体相容皆以内之尖切
　　　　　　　　　　外之面惟立方内容四等面

　　　　　　　　　　则以角而切角立方内容十
　　　　　　　　　　二等面二十等面则以边而
　　　　　　　　　　切面
　
　
　
　
　历算全书卷五十七