钦定四库全书
　历算全书卷六十
　　　　　　　　　　　　　宣城梅文鼎撰
　堑堵测量二
　　总论
堑堵测量者句股法也以西术言之则立三角法也古
九章以立方斜剖成堑堵其两端皆句股再剖之则成
锥体而四面皆句股矣任以锥体之一面平寘为底则

其锐上指环而视之皆成立面之句股而各有三角三
边故谓之立三角也
立三角之法以测体积方圆斜侧靡所不通其测浑圆
之弧度则有二理其一用视法如弧三角所诠用三角
三弧之正弦切线移于平面(谓浑圆立/剖之平面)即成三层句股
相似之比例今谓之浑圆容立三角也其一不用视法
而用实数如句股锥形等法用三弧三角之割线馀弦
各于其平面自成相似之句股以为比例(三弧直剖至/浑圆之心即)

(各成句股/形之面)今谓之堑堵测量也(浑圆内容之立三角亦/堑堵之分形而堑堵测)
(量所测亦浑圆之度因书匪一时所为而/意各有属其名遂别二而一一而二者也)
　　以上通论立三角及堑堵测量命名之意并其同
　　异之处(因立三角有堑堵之名因浑圆内三层句/股生堑堵之用故存此二者以为堑堵测)
　　(量基/本)
凡数之可算者皆可作图以明之故浑圆可变为平圆
如古者盖天之图是也数之可算可图者皆可制器以
象之故浑圆可剖为锥体堑堵测量之仪器是也

凡测算之器至今日大备且益精益简古者浑仪经纬
相结为仪三重至郭太史之简仪立运仪则一环而已
足今则更省之为象限仪是益简益精之效也至于浑
象无与于测而有资于算所以證理也西法之简平浑
盖以平写浑亦可谓工巧之至独未有器以證八线夫
用句股以算浑圆其法莫便于八线然八线之在平圆
者可以图明在浑圆者难以笔显(鼎/)盖尝深思其故而
见浑圆中诸线犁然有合于古人堑堵之法乃以坚楮肖

之为径寸之仪而三弧三角各线所成之句股了了分
明省笔舌之烦以象相告于作圆布算不无小补而又
非若浑象之难成因名之曰堑堵测量从其质也
堑堵形析浑象之一体亦如象限仪割浑仪之一隅环
而测之则象限即浑仪之全周也周遍析之则堑堵即
浑象之全体也是故堑堵形可析为两可合为一其析
者一为句股锥(亦曰立/三角仪)则起二分讫二至一为句股方
锥(亦曰方/直仪)则起二至讫二分起二分者西率起二至者

古率也是两者九十度中皆可为之(自分讫至九十度/并可为句股锥自)
(至讫分九十度并/可为句股方锥)然至半象以上割切三线太长溢出
于方堑堵之外故又有互用之法也其合者近分度用
句股锥近至度用句股方锥以黄道四十七度赤道四
十五度为限过此者互用其馀如是则两锥形合之成
方堑堵矣
方堑堵内又成圆堑堵二其一下为赤道圆象限而一
为撱形之象限距度之割切二线所成也其一下为撱

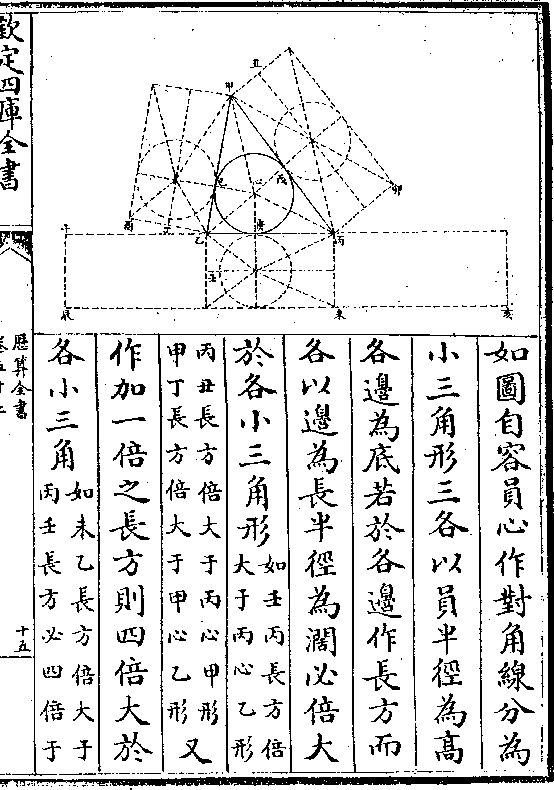形象限而上为黄道之圆象限距度正弦黄道半径所
成也(两圆堑堵之用已/括于两锥形内)两圆堑堵内又以黄道正弦距
度正弦成小方堑堵之象则郭太史圆容方直本法也
于是又有圆容方直仪简法而立三角之仪遂有三式
(一句股锥其形四锐一方直仪其底长方/一圆容方直简法仪其底为浑圆幂之分)
之三者或兼用割切或专用正弦而并不用角合浑圆
内三层句股观之可以明立法之根
　　以上论堑堵测量仪器(句股锥形及句股方锥形/二种为堑堵测量正用而)

　　(圆容方直形专用正弦成小堑堵尤正用中之正/用也此小堑堵在两重圆堑堵内故兼论之又此)
　　(小堑堵足阐授时弧矢/之秘因遂以郭法附焉)
问八线生于角用八线而不用角何也曰角与弧相应
故用角即用弧也用弧即用角也明于斯理而后可以
用角浑圆内三层句股是也明于斯理而后可以不用
角堑堵三仪是也用角者西法也而用角即用弧则通
于古法也不用角者古法也而用弧即用角则通于西
法也于是而古法西法可以观其会通息其烦喙矣

　　以上论角即弧解之理

立三角法序
立三角者量体之法也西学以几何原本言度数而所
译六卷之书止于测面其测体法则未之及盖难之也
余尝以句股法释几何而稍为推广其用谓之几何补
编亦曰立三角法本为体积而设然其中义类颇有与
浑圆弧度之法相通者故摘录之以明堑堵测量之理

立三角法摘录
　　总论
一立三角为有法之形
　立三角之面皆平三角也平三角不拘斜正皆为有
　法之形故立三角亦不拘斜正而皆为有法之形
　
　
一立三角为量体之密率

　凡量体者必析之析之成立三角形则可以知其容
　积可得而量矣若不可以立三角析者则为无法之
　形不可以量
一立三角即锥体
　立三角任以一面平安如底则馀三面皆斜立(亦有/一面)
　(正立/者)而锐必在上即成三角立锥
一各种锥体皆立三角之合形
　凡锥体必上尖下阔任取其一面观之皆斜立之平

　三角也凡锥形自其尖切至底则其中剖之立面亦
　平三角也锥体之底或四边五边以至多边若以对
　角线分其底又即皆成平三角也故四棱锥可分为
　两五棱锥可分为三六棱以上无不可分分之皆立
　三角形故知一切锥体皆立三角之合形也
　
　
　底之边多至于三百六十又析之为分为秒以此为

　底皆可成锥体再析之至于无数即成平员底可作
　员锥要之皆小平三角面无数以成之者也
　
　
一各种有法之形亦皆立三角之合形
　如立方体依其棱剖至心成立分体皆扁方锥其斜
　面辏心皆成立三角长方体亦然
　四等面体从其棱剖至心成四分体八等面则成八

　分体二十等面成二十分体皆立三角锥
　
　
　十二等面依棱剖至心成十二分体皆五棱锥其立
　面五皆立三角
　
　
　浑员形以浑员面幂为底半径为高作大员锥而成

　浑积准前论皆无数立三角所成然则浑员亦立三
　角也
　浑员既为立三角所成则半之而为半浑员(一平员/面一半)
　(浑员面如/员瓜中剖)或再分之而为一象限或更小于象限之
　浑员(细分弧面自象限以内至于一度内若干/分秒如剖橘瓤并一弧面两半平员面)以浑
　员之理通之皆立三角所成
一无法之形有面有棱即皆为立三角所成
　准前论各依其楞线割之至底或依对角线斜剖之

　即皆成立三角而无法之形皆可为有法之形
一立三角体之形不一而皆有三角三边
　非四面不能成体故立三角必四面非三角三边不
　能成面故立三角体之面皆三角三边
　约举其类有四面相等者即四等面形也(其面幂等/其棱之长)
　(短亦/等)
　有三面相等而一面不等者其不等之一面必三边
　俱等馀三棱则自相等

　
　(以上皆形也四等面任以一面为底其雉尖正立居/中三等面形以等边之一面为底锥尖亦正立居中)
　有二面两两相等者
　
　有二面相等馀二面不等者
　
　有四面各不相等者

　有三面非句股而一面成句股者有两面成句股者
　(其句股或/等或否)
　有四面并句股者句股立锥也
　　(以上不皆正形而/皆为有法之形)
一立三角形有实体有虚体
　实者如台如塔如堤虚者如井如池又如隔水测物
　皆自其物之平面角作直线至人目即成虚立锥体
　以人目为其顶锐而所测平面则其底也所作直线

　皆为其棱若所测平面为四边五边以上皆可作对
　角线分为立三角锥形(虚体实体/并同一法)
　立三角又有三平面一弧面者如自地心作三直线
　至星宿所居之度则此三星之相距皆弧度也三弧
　度为边即成弧三角形以为之底其三直线皆大员
　半径以为之棱而合于地心以为之顶锐亦立三角
　之虚形(即弧三/角锥体)
　若于浑球体作三大圈相交成弧三角形从三角作

　直线至员心依此析之即成实体与上法并同一理
一立三角形有立有眠有倒有倚立者以底平安则其
　锐尖上指如人之立
　眠者以底侧立如堵墙而锥形反横如人之眠此惟
　正形之锥则有之(既定一面为底则底在/下者为立在旁者为眠)如虚形则
　不拘正斜皆以所测为底
　又如弧三角锥以浑员面上所成之弧三角为底以
　三直线辏于浑体之心为其顶锐则四面八方皆可

　为底而锐常在心不特能眠能立亦且能倒能欹(亦/惟)
　(有底有锐之正形则然若/他形底无定名随人所置)眠体倒体以及他形之欹
　侧不同而皆为有法之形者三角故也
　
　
一古法有堑堵阳马鳖臑刍甍等法皆可以立三角处
　之(堑堵一/作堑堵)
　凡立方体从其面之一棱依对角斜线剖至其底相

　对之一棱则其积平分而成堑堵形
　　　　(甲乙为顶有袤无广丙丁戊己为方底或长/方则丙丁同巳戊为袤丁己仝丙戊为广乙)
　　　　(丙同甲丁为其高甲丁乙丙为立面甲乙戊/己为斜面皆长方乙丙戊同甲丁巳为两端)
　　　　(立面皆句股形/而相对相等)
　　　　(堑堵形有如屋者甲乙顶袤如屋脊甲乙丙/丁及甲乙戊巳两长方皆斜面而相等丙丁)
　　　　(戊己为底乙丙戊与甲巳丁两圭形相对而/等而以乙辛为其高其辛丙及辛戊俱平分)
　　　　(而/等)
　　　　(又或甲乙顶袤不居正中而近一边然甲乙/与丁丙及巳戊俱平行而等其甲丁乙丙及)

　　　　(甲巳乙戊两斜面虽有大小而并为长方形/乙辛垂线不能分丙辛及辛戊为平分而必)
　　　　(与丙戊底为十字正/角则乙辛为正高)
　以上三者皆堑堵之正形并以高乘底折半见积何
　也皆立方之半体其两端皆立三角形也(第一形两/端为句股)
　(第二第三皆以乙/辛中剖成两句股)
　凡堑堵形亦可立可眠立者以甲乙为顶长丙丁戊
　己为底眠者以戊己为顶长反以甲乙丙丁为底如
　隔水测悬崖之类

　　　　(又有斜堑堵形其各线不必平行底不必正/方但俱直线则底与两斜面皆可作对角线)
　　　　(以分为三角形而诸数可测实体/虚体并有之于测量之用尤多)
　斜堑堵本为无法之形而亦能为有法之形者可析
　之成三角也
　凡堑堵形从顶上一角依对角线斜剖之为两则成
　一立方锥一句股锥
　　　　(堑堵形从乙角作乙巳乙丁两/对角线依线剖之则成两形)
　

　　　　(立方锥一/)　　　　(句股锥一/)
　　　　(名阳马/)　　　　　(名鳖臑/)
　阳马形(以丙丁戊己方形为底以乙为顶锐而偏居/一角故乙丙直立如垂线以为之高其四立)
　(面皆成句股形故/又名句股立方锥)
　论曰阳马形从堑堵第一正形而分故其高线直立
　于一隅乃立方之楞线四面句股形因此而成是为
　句股方锥之正体若斜堑堵等形之分形则但可为
　斜立方锥而不得为句股方锥亦非阳马

　　　　　(斜立方锥者其顶不居正中然又不能正/立一隅故非句股立锥而但为斜立方锥)
　　　　　(如上二形顶既偏侧底亦非方亦斜立锥/形也然其立面皆三角故亦为有法之形)
　　　　　(斜立方锥亦可立可眠皆可以立三角/法御之但不如句股立方锥之有一定)
　　　　　(比/例)
　　　　　鳖臑形(以甲乙为上袤而无广以丁巳为/下广而无袤故称鳖臑象形也其)
　　　　　(各面或句股或不为句股/而皆三角故又名三角锥)
　　　　　句股立锥形(其上有袤而无广下有广而/无袤并同鳖臑所异者甲角)
　　　　　(正方故乙甲丁立面乙甲巳斜面并成句/股又丁角正方故甲丁已平面乙丁巳斜)

　　　　　(面并成句股又丁角正方故甲丁巳平面/乙丁巳斜面并成句股是四面皆句股也)
　　　　　(故谓之句股方锥/而不得仅名鳖臑)
　论曰鳖臑中有句股立锥犹斜立方锥中之有句股
　方雉也立三角皆有法之形而此二者尤可以明测
　量比例之理
　又论曰立三角所以为有法形者谓其可施八线也
　而八线原为句股之比例此二者既通体皆句股所
　成故在有法形中尤为有法矣

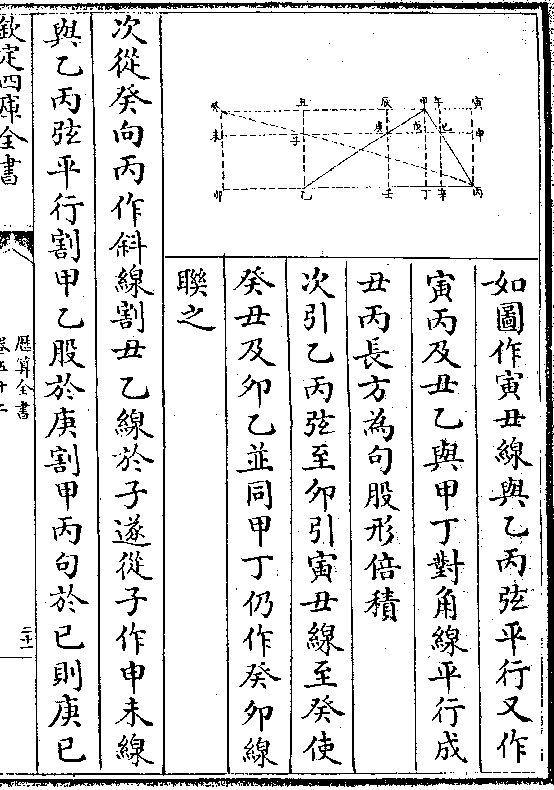　又论曰若于句股方锥再剖之即又成二句股锥而
　皆等积故阳马为立方三之一句股锥则为六之一
　皆立方之分体也
　又论曰句股方锥及句股锥皆生于堑堵故堑堵形
　为测量之纲要
　　(刍薨形亦如屋而两端渐杀故顶窄而底宽其丙/丁戊己底或正方或长方甲乙顶小于丙丁或居)
　　(正中或稍偏然皆与/丙丁及戊己平行)
　刍甍盖取草屋之象乃堑堵形之一种亦可分为三鳖臑

　
　
　
　
　又有刍童者形如方台皆立方之变体方台面与底俱正
　方刍童则长方而面小底大则同亦皆可分为立三角

　准前论方台作对角线并可为两刍甍即可再分为
　六鳖臑即皆立三角锥也
　论曰量面者必始于三角量体者必始于鳖臑皆有
　法之形也量面者析之至三角而止再析之仍三角
　耳量体者析之至鳖臑而止再析之仍鳖臑耳面之
　可以析为三角者即为有法之面体之可以析之为
　鳖臑者即为有法之体盖鳖臑即立三角之异名也
　量体者必以立三角非是则不可得而量

算法
凡算立三角体须求其正高以正高乘底以三而一见
积其法有三其一顶居一角其棱直立即用为正高其
二顶锐不居一角而在三角之间其三顶斜出底三边
之外并以法求其垂线为正高
　　　　假如巳甲乙丙立三角体甲乙丙为底已为
　　　　顶锐正居丙角之上巳丙如垂线为高先以
　　　　乙丙五十六尺甲乙边(六十/一尺)甲丙边(七十/五尺)求

　其羃积(一千六百/三十尺)以乘已丙高(四十/尺)得(六万七千/二百尺)为
　实以三为法除之得(二万二千/四百尺)为立三角锥体若欲
　知已乙甲已两斜弦依句股求弦即得(已丙既直立/则恒为股以)
　(股自乘幂加乙丙句幂为弦幂开方得已乙弦/又以股幂加甲丙句幂为弦幂开方得甲乙弦)
　　　　　若已顶不居一角而在三角之中则已丙
　　　　　非正高乃斜棱也法当分为两形其法依
　　　　　丙已棱直剖至底
　　　　　以上二形乃中剖为二之象其中剖之立

　面亦成丁已丙三角形如平三角法求得已戊垂线
　即为正高如上法先求甲乙丙羃以乘已戊高得数
　为实三除见积
　　　　　又法不必剖形但于形外任依一楞如丙
　　　　　已于庚作垂线至丙以法取庚点与已顶
　　　　　平行即庚丙为正高与己戊等(或量得庚/已横距为)
　　　　　(句以己丙为弦求其股/即得庚丙正高亦同)
　　　　　立三角之顶有斜出者或在底外则于已

　　　　　顶作垂线至庚与甲乙丙底平行乃任用
　　　　　相近一棱如己乙为弦量庚乙之距为句
　　　　　依法求其股得己庚为其正高以乘底三
　　　　　除见积
　问己顶既居形外己庚何以得为正高也曰此易知
　也但补作甲庚虚线成四边形为底则为四棱立锥
　而己庚为其正高甲乙丙底乃其底之分也亦必以
　己庚为正高矣

　　　　　假如乙庚丙甲为底丙甲与乙庚等丙乙
　　　　　与甲庚等或斜方或正方其己庚一棱正
　　　　　立如垂则即为正高正高乘方底三除之
　　　　　即体积也若从甲乙对角线分其底为均
　半又依甲己甲乙二棱从顶直剖之至底则分为两
　三角形而各得其积之半矣(底既平分为两则/其积亦平分为两)其己
　庚乙甲形与己甲乙丙形既皆半积则相等而庚乙
　甲底与甲乙丙底又等则其高亦等而己庚乙甲形

　既以己庚为高矣则己甲乙丙形之高非己庚而何
　又论曰量体积者必先知面犹量面幂者必先知线
　也然则量体者亦先知线矣是故量体之法可转用
　之以求线也(量体者有先知之面幂有求而得之面/幂夫求之而得面者必先求其面幂之)
　(界界即线也故量体之/法可用之以求线也)何谓以量体之法求线曰测
　量是也前论立三角有虚体为测量之用夫虚体者
　无体者无体而有线如实体之有棱故可以量体之
　法求之也如所测之物有三点即成三边三角当以

　三直线测之则立三角锥形矣所测有四点当以四
　直线测之则四棱立锥形矣两测则又为堑堵形矣
　故测量之法可以求线也
　又论曰用立三角以量体者所用者仍平三角也而
　用三角以量面者所用者仍句股也吾以是而知圣
　人立法之精深广大

浑圜内容立三角体法
　　　　　　　全形为堑堵
　　　　　　　分形为鳖臑即立三角体又为句股
　　　　　　　立锥西法所用
　　　　　　　若内切小堑堵则为圜容方直形即
　　　　　　　郭太史弧矢法
先解全形　堑堵体
亢戊乙卯为堑堵斜面　其形长方

　卯乙为浑圜半径(卯为浑/圜之心)亢戊为四十五度切线与
　卯乙同度同为横边　亢卯为乙角割线与戊乙同
　度同为直边
亢氐戊丁为堑堵立面　其形横长方
　亢氐者乙角切线也与戊丁同度以为之高　亢戊
　及氐丁皆四十五度切线与半径同度以为之阔
亢氐卯戊丁乙皆堑堵两和之墙　其形皆立句股
　氐卯同丁乙皆半径为句　亢氐同戊丁皆乙角切

　线为股　亢卯同戊乙皆乙角割线为弦
卯乙丁氐为堑堵之底　其形正方
　卯乙及卯氐皆浑圜半径其对边悉同
法曰先为立方体以容浑球使北极在上南极在下皆
正切于立方底盖之中心则赤道平安而赤道之二分
二至亦皆在立方四面之中心矣
次依赤道横剖方体为均半而用其上半为半立方容
半浑圜形则二分二至皆在半立方之底线各中心而

赤道全圈居其底
次依二分二至从北极十字剖之又成四小立方各得
原立方八之一而小立方内各容浑圜分体八之一
此小立方有一角之楞直立为北极之轴上为北极下
即浑圜心卯角也其立方根皆浑圜半径
次依黄赤道大距取切线为高作横线于小立方夏至
之一边即亢戊线
次依亢戊横线斜剖至对边之足则成堑堵矣(对边之/足即卯)

(乙也本为黄赤道半径今在小/立方体为方底之边故云足也)
堑堵体有五面　其一斜面(亢戊乙/卯长方)　其三立面(一亢/氐戊)
(丁长方二亢氐卯戊/丁乙相等两句股)　其一方底(卯乙氐/丁平方)
　
　
　
　
　

堑堵形面　有赤道象弧在方底　有黄赤大距弧在
立句股边　即两和之墙
底形　　　　　底形正方　其卯角即黄赤道心
　　　　　　　氐甲乙为赤道一象限　乙为春分
　　　　　　　　氐为夏至赤道　卯氐及卯乙皆
　　　　　　　赤道半径　其对边氐丁及乙丁皆
　　　　　　　四十五度切线

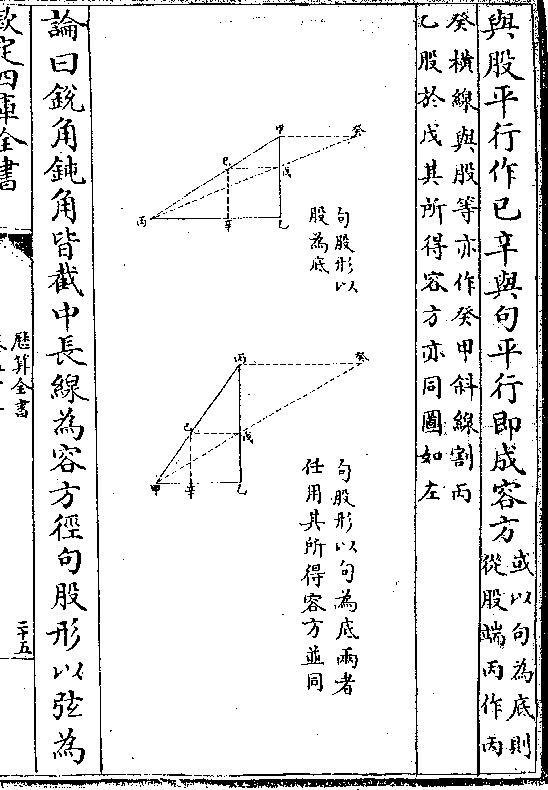立句股面形一　　立句股之面有二(一亢氐卯/一戊丁乙)皆同角
　　　　　　　　同边　亢氐卯形内有氐癸弧为夏
　　　　　　　　至黄赤大距二十三度半强　氐卯
　　　　　　　　为赤道半径　癸卯为黄道半径
　　　　　　　　卯角为黄赤大距角(氐癸弧/之角)　亢氐
　　　　　　　　者氐癸弧之切线(亦即卯/角切线)　亢卯者
　　　　　　　　氐癸弧之割线(亦即卯/角割线)
　

癸弧之割线(亦即卯/角割线)
立句股面形二　戊乙丁形即前图亢氐卯形之对面
　　　　　　　　戊丁高同亢氐切线(如/股)　戊乙斜
　　　　　　　线同亢卯割线(如/弦)　丁乙横线同氐
　　　　　　　卯(如/句)　乙角同卯角

又有黄道象弧在斜面
斜面形　　　　斜面形长方(其斜立之/势依黄道)　其卯角为
　　　　　　　黄道心(即赤/道心)　乙丙癸为黄道一象
　　　　　　　限　乙为春分(与赤道/同用)　癸为黄道
　　　　　　　夏至　卯癸及卯乙皆黄道半径(内/卯)
　　　　　　　(乙与赤/道同用)　亢卯为二十三度半强之
割线(夏至黄赤/大距割线)　其相对戊乙边与亢卯割线同度
亢戊边与卯乙半径相对同度乃四十五度之切线(与/底)

(上切线氐/丁相应)
立面形　　　　立面形亦长方其势直立　亢戊及
　　　　　　　氐丁二边为其阔皆四十五度切线
　　　　　　　与半径同度　亢氐及戊丁为其高
　　　　　　　皆二十三度半之切线(夏至黄赤/大距切线)
　　　　　　　以亢戊边庋起斜面之亢戊边而成
　　　　　　　角体仍以氐丁边联于方底之氐丁
　　　　　　　边则其形直立矣

　
　
　
次解分形　立三角体(古谓鳖臑/即句股锥)
内含乙甲丙弧三角形及乙甲丙卯弧三角锥
卯为浑圜心(黄赤/同用)　卯乙浑圜半径(黄赤/同用)　乙丙弧为
黄道经度　丙卯为黄道半径　乙甲弧为赤道经度
　甲卯为赤道半径　丙甲弧为黄赤距纬　乙为春

分点　酉乙未角为春分角二十三度半与二至大距
之纬度相应此角不动　丙为所设黄道度距春分后
之点此点移则丙之交角变而诸数皆从之而变
法曰于前图全形堑堵斜面黄道象弧内寻所设黄道
经度自春分(乙/)起数设度至丙从丙向圜心卯作丙卯
半径遂依半径引长至堑堵之边(酉/)成酉卯直线依酉
卯直线直剖至底(未卯线为底/酉未线为边)成酉未乙卯立三角体
此立三角体有四面而皆句股故又曰句股立锥

立句股之锥尖为酉
其斜面为酉乙卯句股形(乙正角句乙酉为股弦/乙卯为 酉卯为)
其立面二
　一为酉未乙句股形(未正角句酉未垂线为股/未乙为 酉乙为弦)
　一为酉未卯句股形(未正角句酉未垂线为股/未卯为 酉卯为弦)
其底为未乙卯句股形(乙正角句未乙为股弦/乙卯为 未卯为)
　　以上四句股面凡楞线六
卯乙半径也酉乙黄道丙乙弧之切线也而酉卯则其

割线也未乙赤道乙甲弧之切线也而未卯则其割线
也惟酉未垂线于八线无当今名之曰锥尖垂线亦曰
锥尖柱亦曰外线以其离于浑圜之体也
句股面有四而用者一酉未乙也以其能与乙角之大
句股为比例也
楞线六而用者二酉乙及未乙也以其为二道之切线
为八线中有定数可为比例也
第一层句股比例图

　　　　　酉未乙句股形以黄道切线(酉/乙)赤道切线
　　　　　(未/乙)相连于乙角(成锐/角)则酉乙为弦未乙为
　　　　　句而戊丁乙及牛昴乙二句股形同在一
　　　　　立面又同用乙角故可以相为比例
　　　　　术为以赤道半径(丁/乙)比乙角之割线(戊/乙)若
　　　　　赤道切线(未/乙)与黄道切线(酉/乙)也(此为以/句求弦)
　　　　　又以黄道半径(牛/乙)比乙角之馀弦(昴/乙)若黄
　　　　　道切线(酉/乙)与赤道切线(未/乙)也(此为以/弦求句)

解曰丁乙与氐昴同大则皆赤道半径也戊乙与亢卯
同大则皆乙角割线也牛乙与癸卯同大皆黄道半径
昴乙与己卯同大皆乙角馀弦也　从乙窥卯则成一
点而乙角卯角合为一角其角之割线馀弦尽移于堑
堵之第一层而同在一立面为句若弦(观总图/自明)
　以赤道求黄道　　以黄道求赤道
一　赤道半径　　一　黄道半径
二　乙角割线　　二　乙角馀弦

三　赤道切线　　三　黄道切线
四　黄道切线　　四　赤道切线
　若求角者反用其率　　　　又法
　
　
　
四　乙角割线　　　　　四　乙角馀弦
第二层句股比例图

　　　　　子甲丑句股形以黄赤距度之切线(子/甲)赤
　　　　　道之正弦(甲/丑)相连于甲成正角则子甲为
　　　　　股甲丑为句而与坎震丑及女娄丑二句
　　　　　股形同在一立面又同丑角故可相求
　　　　　术为以赤道半径(震/丑)比乙角之切线(坎/震)若
　　　　　赤道正弦(甲/丑)与距度之切线(子/甲)也(是为以/句求股)
　　　　　又为以乙角之正弦(女/娄)与乙角馀弦(娄/丑)若
　　　　　距度之切线(子/甲)与赤道之正弦(甲/丑)也(是为/以股)

　(求/句)
解曰震丑即氐卯赤道半径也坎震即亢氐乙角之切
线也女娄即癸己而娄丑即己卯乙角之正弦馀弦也
　从乙窥卯则乙丑卯成一点而合为一角其角之切
线正弦馀弦尽移于堑堵第二层立面为句与股
　以赤道求距度　以距度求赤道　又法
一　半径　　　一乙角正弦　一乙角切线　半径
二　乙角切线　二乙角馀弦　二半径　　　(乙角/馀切)

三　赤道正弦　三距度切线　三　距度切线
四　距度切线　四赤道正弦　四　赤道正弦
　若求角则反用其率　　　又法
一　距道切线　半径　　一　赤道正弦　半径
二　赤道正弦　　　　　二　距度切线
三　半径　　　(距度/馀切)　　三　半径　　　(赤道/馀割)
四　乙角馀切　　　　　四　乙角切线
第三层句股比例图

　　　　　丙辛壬句股形以距度正弦(丙/辛)黄道正弦
　　　　　(丙/壬)相连于丙而成锐角则丙壬为弦丙辛
　　　　　为股而与乾艮壬及奎胃壬二句股同在
　　　　　一立面同用壬角故可相求
　　　　　术为以黄道半径(奎/壬)比乙角之正弦(奎/胃)若
　　　　　黄道正弦(丙/壬)与距度之正弦(丙/辛)也(是为以/弦求股)
　　　　　又为以乙角之切线(乾/艮)比乙角之割线(乾/壬)
　　　　　若距度之正弦(丙/辛)与黄道正弦(丙/壬)也(是为以/股求弦)

解曰奎壬即癸卯黄道半径也奎胃即癸己距度正弦
也乾艮即亢氐而乾壬即亢卯则乙角之切线割线也
　从乙窥卯则乙丑壬卯半径因直视成一点而合为
为一角其角之正弦切割线尽移于堑堵之第三层立
面以为弦为股
　以黄道求距度　　以距度求黄道　又法
一　半径　　　一　乙角切线　一　乙角正弦　半径
二　乙角正弦　二　乙角割线　二　半径　　　(乙角/馀割)

三　黄道正弦　三　距度正弦　三　距度正弦
四　距度正弦　四　黄道正弦　四　黄道正弦
　若求角则反用其率　　　　又法
一　距度正弦　半径　　一　黄道正弦　半径
二　黄道正弦　　　　　二　距度正弦
三　半径　　　(距度/馀割)　　三　半径　　　(黄道/馀割)
四　乙角正割　　　　　四　乙角正弦
弧三角锥体(即割浑圜/体之一分)

　
　
　
　
法曰依前论从丙点对卯直割至底则截黄道于丙截
赤道于甲得丙乙及甲乙二弧所剖浑圜之迹又成丙
甲弧(为两道/距纬)三弧相凑成丙甲乙弧三角面　丙卯甲
卯乙卯同为半径三半径为楞辏于卯心卯为三角之

尖乙甲丙弧三角面为底成乙甲丙卯弧三角锥体为
割浑圜体之一分也
此弧三角锥体含于句股立锥体内准前论可以明之
因此弧三角锥与句股锥同锐(卯/尖)异底(一以弧三角面/为底一以句股)
(平面/为底)故以弧三角变为句股以求其比例而有三法(即/前)
(条所论三/层句股)
其一为酉未乙句股形
　用酉乙弦(为黄道丙/乙弧切线)未乙句(为赤道乙/甲弧切线)以当乙角之

　弦与句
其一为子甲丑句股形
　用子甲股(为距度丙/甲弧切线)甲丑句(为赤道乙/甲弧正弦)以当乙角之
　股与句
其一为丙辛壬句股形
　用丙辛股(为距度丙/甲弧在弦)丙壬弦(为黄道丙/乙弧正弦)以当乙角之
　股与弦
问两弧求一弧非句股锥乎与此所用同耶异耶曰形

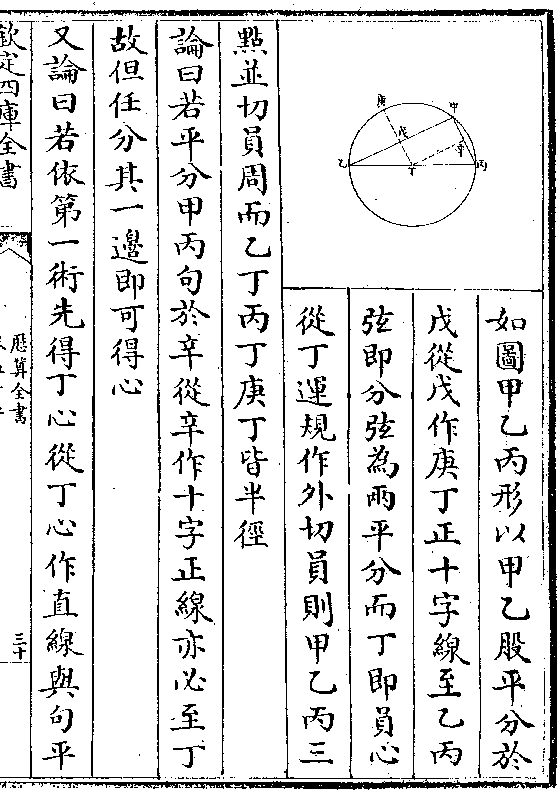不异也乃法异耳何言乎法异曰句股锥一也而有用
角不用角之殊此用角度其句股在锥形之底(以卯心/为锥形)
(之锐则三层句/股皆为其底)而遥对浑体之心以视法成比例两弧
求一弧不用角度其句股同在锥形之一面无假视法
自成比例所以不同然其为句股之比例一而已矣
然则两弧求一弧惟用割线馀弦此所用者惟正弦切
线又何不同若是耶曰角之句股在心(如卯亢氐等形/皆依极至交圈)
(平剖浑圜成平面其象/始著是在浑圜之心)与为比例之句股在面(如酉未/乙等形)

(皆以一角连/于浑圜之面)二者相离以视法相叠如一平面然惟正
弦切线能与之平行(从凸面平视则设度之正弦切线/皆与浑圜中割之平面诸线平行)
若割线馀弦皆非平行因视法而跻缩失其本象(或斜/对则)
(长线成短线或对/视则直线成一点)不能为比例无所用之矣若两弧求
一弧则其句股自相垛叠于一平面(平立斜三面各具/三句股而如相垛)
(叠并以一大句/股横截成三)皆以本数自相为比例全不关于视法
故无跻缩而其算皆割线馀弦所成于正弦切线反无
所取所以不同　若以量体之法言之割线馀弦为量

立楞斜楞之法正弦切线则量底之法也(两弧求一弧/法见二卷)
　　　　　　　　　　　　如图　以卯为句股立
　　　　　　　　　　　　锥之顶卯乙为直立之
　　　　　　　　　　　　楞如浑圆半径卯未卯
　　　　　　　　　　　　酉为斜面之楞并如割
　　　　　　　　　　　　线酉乙未乙两底线并如
　　　　　　　　　　　　切线若依底线平截之成
　　　　　　　　　　　　大小三形则比例见矣

剖浑圜用馀度法
　　　　　　　　　　　　乙丙黄道弧在四十五
　　　　　　　　　　　　度以上求甲乙赤道弧
　　　　　　　　　　　　(即同/升度)
　　　　　　　　　　　　依前法　半径(癸卯亦/即庚乙)
　　　　　　　　　　　　与乙角(春/分)之馀弦(乙壬/亦即)
　　　　　　　　　　　　(卯/己)若乙丙(黄/道)之切线(尾/乙)
　　　　　　　　　　　　与乙甲(赤/道)之切线(箕/乙)

此法无误但如此则两切线大于堑堵须引之于形外
是以小比例例大比例也若至八十度切线太大不可
作图矣
今改用馀度　法自卯浑圜心遇黄道设弧丙作线至
酉(剖至/底)
　以乙丙黄道之馀弧癸丙取其切线于斜面如癸斗
　　又以乙甲赤道之馀弧甲氐取其切线于底如氐
　未即以氐未移至斜面之楞如亢酉变立句股(尾箕/乙)

　为平斜句股(酉亢卯及斗癸/卯两形皆相似)　法为半径(癸/卯)与乙角
　之正割线(乙角即卯角其割/线戊乙亦即卯亢)若乙丙黄道之馀切线
　(癸/斗)与乙甲赤道之馀切线也(亢酉亦/即氐未)
按此法从亢戊边剖堑堵成句股方锥之眠体
　其剖形以亢氐酉未长方形为底以卯为锥尖以斜
　面之卯亢酉句股形及平面之卯氐未句股形为相
　对之二边又以卯氐亢之立面句股形及卯未酉之
　斜立面句股形为相对之二边其四面皆句股其底

　长方而以卯为尖故曰眠形
　不直曰方锥者以面皆句股而卯氐线正立故不得
　仅云阳马谓之句股方锥可也亦如句股锥立三角
　不得仅谓鳖臑

　堑堵测量二
句股锥形序(即两弧/求一弧)
正弧三角之法即郭太史侧视图也郭法以侧视取立
句股又以平视取平句股故有圆容方直之法而不须
用角西法专以侧视之图为用故必用角用角即用弧
也惟其用角故所用者皆侧立之句股也余此法则兼
用平立斜三种句股而其大小句股之比例并在一平
面尤为明白易见而不更言角既与授时之法相通其

兼用割线起算春分又西历之理也盖义取适用原无
中外之殊笇不违天自有源流之合敬存此稿以质方
来其授时历侧视平视之图详具别卷

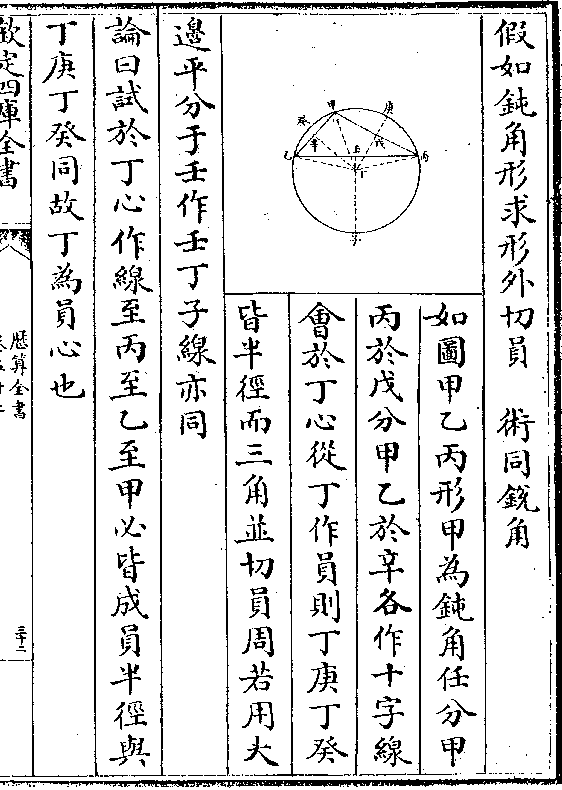
正弧三边形以两弧求一弧法(句股锥形之理/)
　用割线馀弦以弧度求弧度而不言角其理与郭法
　相通
　　　　　　　丙甲乙三角弧形　甲为正角
　　　　　　　卯为浑员心丙乙为黄道距春分之
　　　　　　　一弧甲乙为赤道同升之弧丙甲为
　　　　　　　黄赤距度(即过极圈/之一弧)丙卯为黄道半
　　　　　　　径甲卯为赤道半径卯乙为黄赤两

道之半径壬卯为丙乙黄道之馀弦(以丙壬为/其正弦故)丑卯为
甲乙赤道之馀弦(以甲丑为/其正弦故)辛卯为丙甲距度之馀弦
(以丙辛为/其正弦故)子卯为丙甲割线(以子甲为/切线知之)酉卯为丙乙割
线(以酉乙为/切线如之)未卯为甲乙割线(以未乙为/切线知之)
斜面酉乙卯及子丑卯及丙壬卯皆句股形乙丑壬皆
正角又同用卯角角之弧为丙乙黄道　平面未乙卯
及甲丑卯及辛壬卯皆句股形乙丑壬皆正角又同用
卯角角之弧为甲乙赤道　立面酉未卯及子甲卯及

丙辛卯皆句股形未甲辛皆正角又同用卯角角之弧
为丙甲距度(其又一立面酉未乙及子甲丑及丙辛/壬三句股形为切线正弦所作兹不论)
论曰因诸线成平面句股形为底两立面句股形为墙
斜面句股形为面则四面皆句股形矣而酉未联线及
子甲切线丙辛正弦皆直立上对天顶下指地心故谓
之句股锥形也既成句股则其相等之比例可以相求
　用法
半径与赤道之馀弦若黄道之割线与距度之割线

　
　
　
　
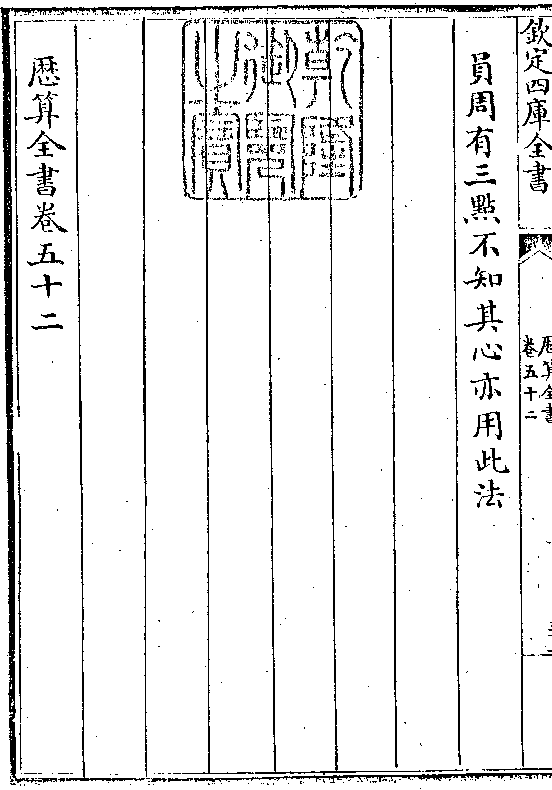
反之则赤道馀弦与半径若距度割线与黄道割线
一　甲乙馀弦　丑卯小句　二　半径　　　乙卯大句
三　丙甲割线　子卯小弦　四　丙乙割线　酉卯大弦
又更之则黄道割线与半径若距度割线与赤道馀弦

一　丙乙割线　酉卯大弦　二　半径　　　乙卯大句
三　丙甲割线　子卯小弦　四　甲乙馀弦　丑卯小句
　右取斜面酉乙卯子丑卯两句股形以乙卯半径为
　比例偕一馀弦两割线而成四率
半径与距度之割线若黄道之馀弦与赤道之馀弦
一　半径　　　丙卯小弦　二　丙甲割线　子卯大弦
三　丙乙馀弦　壬卯小句　四　甲乙馀弦　丑卯大句
反之则距度割线与半径若赤道馀弦与黄道馀弦

一　丙甲割线　子卯大弦　二　半径　　　丙卯小弦
三　甲乙馀弦　丑卯大句　四　丙乙馀弦　壬卯小句
又更之则黄道馀弦与半径若赤道馀弦与距度割线
一　丙乙馀弦　壬卯小句　二　半径　　　丙卯小弦
三　甲乙馀弦　丑卯大句　四　丙甲割线　子卯大弦
　右取斜面丙壬卯子丑卯二句股形以丙卯半径偕
　一割线两馀弦而成四率
半径与赤道割线若距度割线与黄道割线

　
　
　
　
更之则赤道割线与半径若黄道割线与距度割线
一　甲乙割线　未卯大句　二　半径　　　甲卯小句
三　丙乙割线　酉卯大弦　四　丙甲割线　子卯小弦
又更之则距度割线与半径若黄道割线与赤道割线

一　丙甲割线　子卯小弦　二　半径　　　甲卯小句
三　丙乙割线　酉卯大弦　四　甲乙割线　未卯大句
　右取立面酉未卯子甲卯二句股形以甲卯半径偕
　三割线而成四率
半径与黄道馀弦若赤道割线与距弧馀弦
一　半径　　　乙卯大句　二　丙乙馀弦　壬卯小句
三　甲乙割线　未卯大弦　四　丙甲馀弦　辛卯小弦
更之则黄道馀弦与半径若距弧馀弦与赤道割线

一　丙乙馀弦　壬卯小句　二　半径　　　乙卯大句
三　丙甲馀弦　辛卯小弦　四　甲乙割线　未卯大弦
又更之则赤道割线与半径若距弧馀弦与黄道馀弦
一　甲乙割线　未卯大弦　二　半径　　　乙卯大句
三　丙甲馀弦　辛卯小弦　四　丙乙馀弦　壬卯小句
　右取平面未乙卯辛壬卯二句股形以乙卯半径偕
　两馀弦一割线而成四率
半径与距度馀弦若赤道馀弦与黄道馀弦

　
　
　
　
更之则距度馀弦与半径若黄道馀弦与赤道馀弦
一　丙甲馀弦　辛卯小弦　二　半径　　　甲卯大弦
三　丙乙馀弦　壬卯小句　四　甲乙馀弦　丑卯大句
又更之则赤道馀弦与半径若黄道馀弦与距度馀弦

一　甲乙馀弦　　丑卯大句　二　半径　　　甲卯大弦
三　丙乙馀弦　　壬卯小句　四　丙甲馀弦　辛卯小弦
　右取平面(甲丑卯/辛壬卯)二句股以甲卯半径偕三馀弦而成四率
半径与黄道割线若距弧馀弦与赤道割线
　
　
　
　

更之则黄道割线与半径若赤道割线与距弧馀弦
一　丙乙割线　酉卯大弦　二　半径　　　丙卯小弦
三　甲乙割线　未卯大句　四　丙甲馀弦　辛卯小句
又更之则距弧馀弦与半径若赤道割线与黄道割线
一　丙甲馀弦　辛卯小句　二　半径　　　丙卯小弦
三　甲乙割线　未卯大句　四　丙乙割线　酉卯大弦
　右取立面酉未卯丙辛卯二句股形以丙卯半径偕
　两割线一馀弦而成四率

　作立三角仪法(即句股锥形/)
法以坚楮依各线画成句股而摺辏之则各线之在浑
员者具可睹矣　任取黄道之一弧为例则各弧并同
　　　　　　　　　　　底上甲乙弧赤道同升度
　　　　　　　　　　　也赤道各线俱在平面为
　　　　　　　　　　　底面上丙乙弧黄道度也
　　　　　　　　　　　黄道各线俱在斜面立面
　　　　　　　　　　　丙甲弧度黄赤距纬也距

纬各线俱在立面　外立面为黄赤两切线之界
论曰此即郭若思太史员容方直之理也太史法从二
至起算先求大立句股依距至黄道度取其正半弦为
界直切至赤道平面截黄赤道两半径成小立句股以
此为法求得平面大句股则赤道之正半弦也其直切
两端下垂之迹在二至半径者既成小立句股其在所
求本度者又成斜立句股此斜立句股之股则本度黄
赤距度之正半弦也于是直切之迹有黄道正半弦为

其上下之横长有黄赤距度之正半弦为两端之直阔
成直立之长方形而在浑体之中故曰弧容直阔也此
侧立长方之四角各有黄赤道之径为其楞以直凑浑
体之心成眠体之句股方锥句股方锥者底虽方而锥
尖偏在一楞则其四面皆成句股此郭太史之法也今
用八线之法以句股御浑体其意略同但其法主于用
角故从二分起算遂成立句股锥形立句股锥形亦可
以卯心为锥尖是为眠体锥形如此则两锥形之尖皆

在员心(一郭法/一今法)而可通为一法是故用郭太史法则以
句股方锥为主而句股锥形其馀度所成之馀形今以
句股锥形为主则员容直阔所成句股方锥又为馀度
馀形矣然则此两法者不惟不相违而且足以相法古
人可作固有相视而笑莫逆于心者矣余窃怪夫世之
学者入主出奴不能得古人之深而轻肆诋诃者皆是
也吾安得好学深思其人与之上下其议哉

句股方锥序
堑堵虚形以测浑员原有二法一为句股锥形一为句
股方锥其句股锥之法向有法方锥之法亦略见于
诸篇而未畅厥旨故复著之其法以弧求弧而不求角
与句股锥同而起算二至则郭太史本法矣方锥与锥
形互相为正馀故亦可以算距分之度也

算黄赤道及其距纬以两弧求一弧又法(用句股方锥形/亦堑堵形之分)
　以八线法立算起数二至本郭法史员容方直之理
　而稍广其用亦不言角
　　　　　　　　　　如图癸为二至黄道癸丙为
　　　　　　　　　　距至黄道之一弧(如所/设)氐为
　　　　　　　　　　二至赤道氐甲为距至赤道
　　　　　　　　　　之一弧(与癸丙黄/道相应)癸氐为二
　　　　　　　　　　至黄赤大距弧(二十三/度半强)丙甲

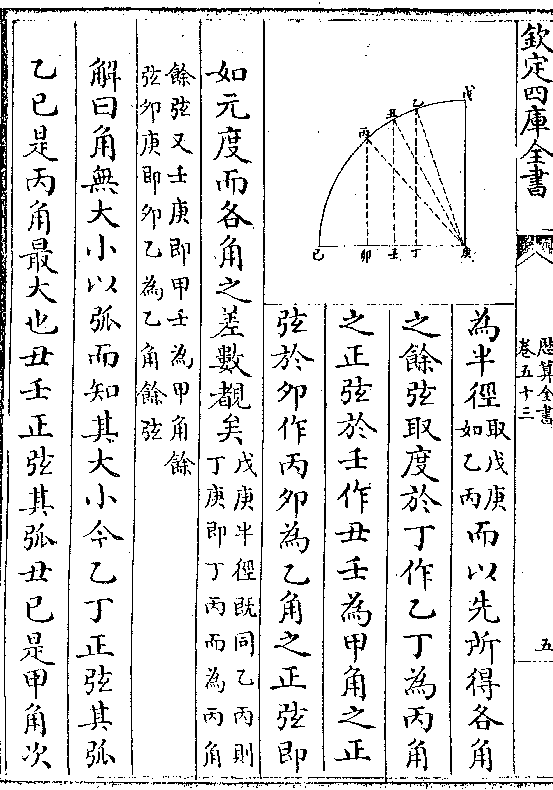为所设各度之黄赤距纬(即过极圈/之一弧)卯为浑圆心
黄道癸丙之正弦丙张馀弦张卯正矢癸张切线癸斗
割线斗卯
赤道氐甲之正弦甲庚馀弦庚卯正矢氐庚切线氐室
割线室卯
大距度癸氐之正弦癸己馀弦己卯正矢氐己切线氐
亢割线亢卯
距纬丙甲之正弦丙辛馀弦辛卯正矢甲辛切线甲子

割线子卯
论曰因诸线成各句股形为句股方锥之面其锐尖皆
会于卯心又成方直形以为之底遂成句股方锥之眠
体
一斜平面有黄道弧诸线成句股形二(一丙张卯/一斗癸卯)又有
　相应之赤道诸线亦成句股形二(一壁亢卯/一子房卯)四者皆
　形相似而比例等
一平面有赤道弧诸线成句股二(一甲庚卯/一室氐卯)又有相应

　之黄道诸线亦成句股二(一辛井卯/一亥己卯)四者皆形相似
　而比例等
一立面有大距弧诸线成句股二(一癸己卯/一亢氐卯)又有相对
　之距纬诸线亦成句股二(一张井卯/一房庚卯)四者皆形相似
　而比例等
一斜立面有黄赤距度诸线成句股二(一丙辛卯/一子甲卯)又有
　相对之大距度诸线亦成句股二(一斗亥卯/一壁室卯)四者皆
　形相似而比例等

论曰斜平面平面立面斜立面各具四句股而并为相
似之形者皆以一大句股截之成四也其股与弦并原
线而所截之句又平行其比例不得不等
一内外两方直形(一在浑员形内即郭法所用乃黄道/及距纬两正弦所成一在浑员形外)
　(乃赤道及大距/两切线所成)有平立诸线为各相似相连句股形
　之句亦即为相似两方锥之底而比例等
一不内不外两方直形(一跨黄道内外乃赤道正弦及/距纬切线所成一跨赤道内外)
　(乃黄道切线及/大距正弦所成)有平立诸线为各相似相连句股形

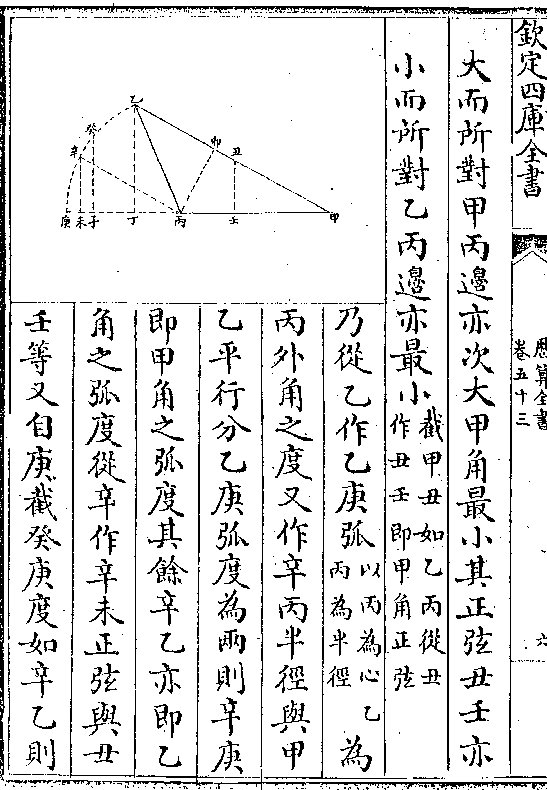　之句亦即为相似两方锥之底而比例等
论曰方锥眠体以平行之底横截之(即四种方直形/皆方锥之底)成
大小四方锥其锥体之顶锐(卯/)与其四棱皆不动所截
之底又平行故其比例相似而等
又论曰黄道在斜平面赤道在平面而其线互居者以
方直形故也大距度在立面距纬度在斜立面而其线
毕具者亦以方直形故也盖形既方直则横线直线两
两相对而等

　用法
斜平面比例
黄道半径与黄道正弦若距纬割线与赤道正弦
　
　
　
　
更之黄道正弦与黄道半径若赤道正弦与距纬割

线
一丙张小股　二丙卯小弦　三子房大股　四子卯大弦
又更之距纬割线与黄道半径若赤道正弦与黄道正
弦
一子卯大弦　二丙卯小弦　三子房大股　四丙张小股
　右取斜平面张丙卯房子卯二句股形以丙卯半径
　偕一割线两正弦而成四率
黄道半径与黄道切线若大距割线与赤道切线

　
　
　
　
更之黄道切线与黄道半径若赤道切线与大距割线
一癸斗小股　二癸卯小句　三亢壁大股　四亢卯大句
又更之大距割线与黄道半径若赤道切线与黄道切线
一亢卯大句　二癸卯小句　三亢壁大股　四癸斗小股

　右取斜平面斗癸卯壁亢卯二句股形以癸卯半径
　偕一割线两切线而成四率
平面比例
赤道半径与赤道正弦若距纬馀弦与黄道正弦

更之赤道正弦与赤道半径若黄道正弦与距纬馀弦
一甲庚大股　二甲卯大弦　三辛井小股　四辛卯小弦
又更之距纬馀弦与赤道半径若黄道正弦与赤道正
弦
一辛卯小弦　二甲卯大弦　三辛井小股　四庚甲大股
　右取平面井辛卯庚甲卯二句股形以甲卯半径偕
　一馀弦两正弦而成四率
赤道半径与赤道切线若大距馀弦与黄道切线

　
　
　
　
更之赤道切线与赤道半径若黄道切线与大距馀弦
一氐室大股　二氐卯大句　三己亥小股　四己卯小句
又更之大距馀弦与赤道半径若黄道切与赤赤道切线
一己卯小句　二氐卯大句　三己亥小股　四氐室大股

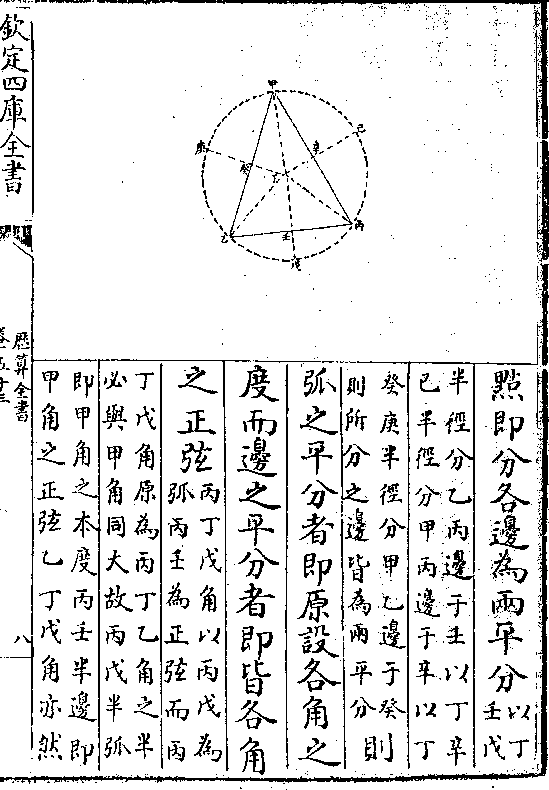　右取平面亥己卯室氐卯二句股形以氐卯半径偕
　一馀弦两切线而成四率
立面比例
黄道半径与大距正弦若黄道馀弦与距纬正弦
　
　
　
　

更之大距正弦与黄道半径若距纬正弦与黄道馀弦
一癸己大股　二癸卯大弦　三张井小股　四张卯小弦
又更之黄道馀弦与黄道半径若距纬正弦与大距正
弦
一张卯小弦　二癸卯大弦　三张井小股　四癸己大股
　右取立面己癸卯井张卯二句股形以癸卯半径偕
　一馀弦两正弦而成四率
赤道半径与大距切线若赤道馀弦与距纬切线

　
　
　
　
更之大距切线与赤道半径若距纬切线与赤道馀弦
一氐亢大股　二氐卯大句三庚房小股　四庚卯小句
又更之赤道馀弦与赤道半径若距纬切线与大距切线
一庚卯小句　二氐卯大句三庚房小股　四氐亢大股

　右取立面房庚卯亢氐卯二句股形以氐卯半径偕
　一馀弦两切线而成四率
斜立面比例
黄道半径与距纬正弦若黄道割线与大距正弦

更之距纬正弦与黄道半径若大距正弦与黄道割线
一丙辛小股　二丙卯小弦　三斗亥大股　四斗卯大弦
又更之黄道割线与黄道半径若大距正弦与距纬正
弦
一斗卯大弦　二丙卯小弦　三斗亥大股　四丙辛小股
　右取斜立面辛丙卯亥斗卯二句股形以丙卯半径
　偕一割线两正弦而成四率
赤道半径与距纬切线若赤道割线与大距切线

　
　
　
　
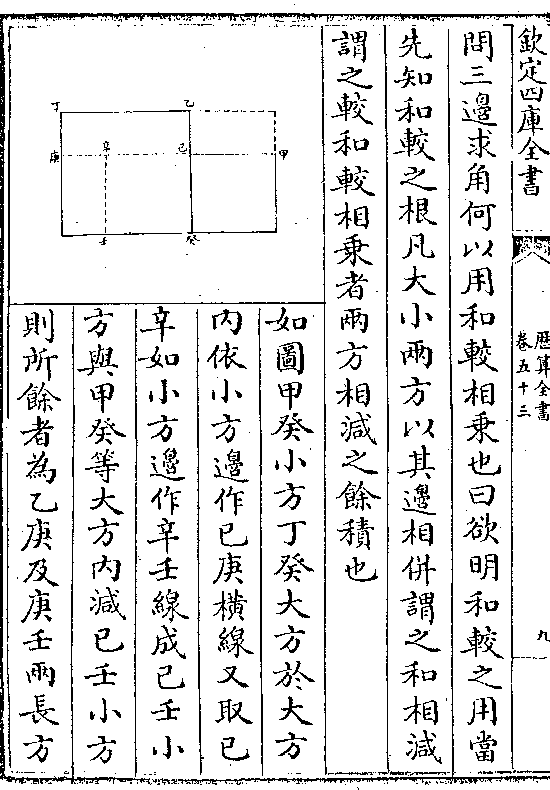
更之距纬切线与赤道半径若大距切线与赤道割线
一甲子小股　二甲卯小句　三室壁大股　四室卯大句
又更之赤道割线与赤道半径若大距切线与距纬切
线

一室卯大句　二甲卯小句　三室壁大股　四甲子小股
　右取斜立面子甲卯壁室卯二句股形以甲卯半径偕
　一割线两切线而成四率
　　以上方锥形之四面每面有大小四句股形即各
　　成四率比例者六合之则二十有四并以两弧求
　　一弧而不言角
方直形比例
黄道正弦与距纬正弦若赤道切线与大距切线

　
　
　
　
更之距纬正弦与黄道正弦若大距切线与赤道切线
一张井小股　二井辛小句　三亢氐大股　四氐室大句
又更之赤道切线与大距切线若黄道正弦与距纬正
弦

一氐室大句　二亢氐大股　三井辛小句　四张井小股
再更之大距切线与赤道切线若距纬正弦与黄道正
弦
一亢氐大股　二氐室大句　三张井小股　四井辛小句
　右取浑体内所容方直形上黄道及距纬两正弦偕
　浑体外所作方直形上赤道及大距两切线而成四
　率
赤道正弦与距纬切线若黄道切线与大距正弦

　
　
　
　
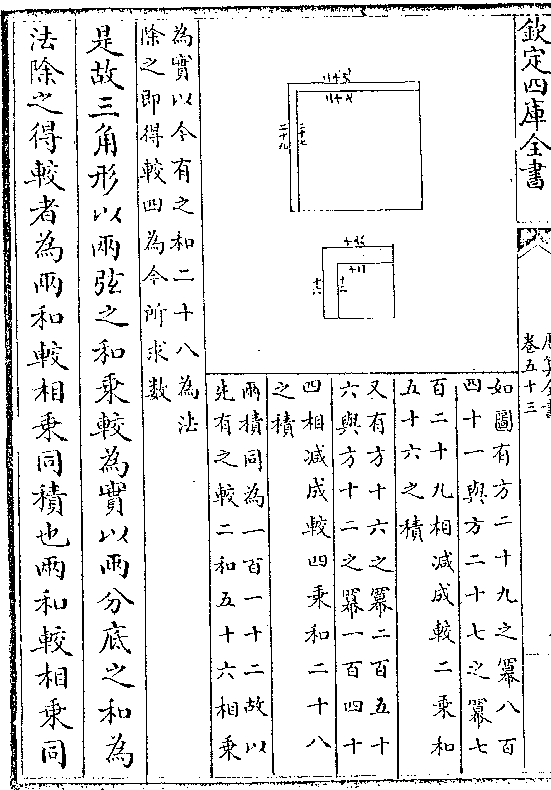
更之距线切线与赤道正弦若大距正弦与黄道切线
一房庚小股　二庚甲小句　三癸己大股　四己亥大股
又更之黄道切线与大距正弦若赤道正弦与距纬切
线

一己亥大句　二癸己大股　三庚甲小句　四房庚小股
再更之大距正弦与黄道切线若距纬切线与赤道正弦
一癸己大股　二己亥大句　三房庚小股　四庚甲小句
　右取方直形上黄道切线大距正弦偕又一方直形
　上赤道正弦距纬切线而成四率
　　以上大小方锥形之底各成方直形而两两相偕
　　即各成四率比例者四合之则八并以三弧求一
　　弧而不言角

　　凡句股方锥形所成之四率比例共三十有二皆不
　　言角内四率中有半径者二十四并两弧求一弧四
　　率中无半径者八以三弧求一弧其不言角则同
问各面之句股形并以形相似而成比例若方直形所
用皆各形之大小句然不同居一面又非相似之形何
以得相为比例曰句股形一居平面一居立面而能相
比例者以有棱线为之作合也何以言之如亢卯割线
为方锥形之一棱而此线既为斜平面句股形(壁亢/卯)之

股又即为立面句股形(氐亢/卯)之弦故其比例在斜平面
为亢卯与张卯若亢壁与张丙也而在立面为亢卯与
张卯若亢氐与张井也合而言之则亢壁与张丙亦若
亢氐卯与张井馀仿此
问此以方直相比非句股本法矣曰亦句股也试平置
方锥(以方底著地使卯锐直指天/顶而卯氐棱线正立如垂)而从其卯顶俯视之
则卯井庚己氐棱线上分段之界因对视而成一点亢
卯棱线与亢氐线相叠室卯线与室氐相叠皆吻合为

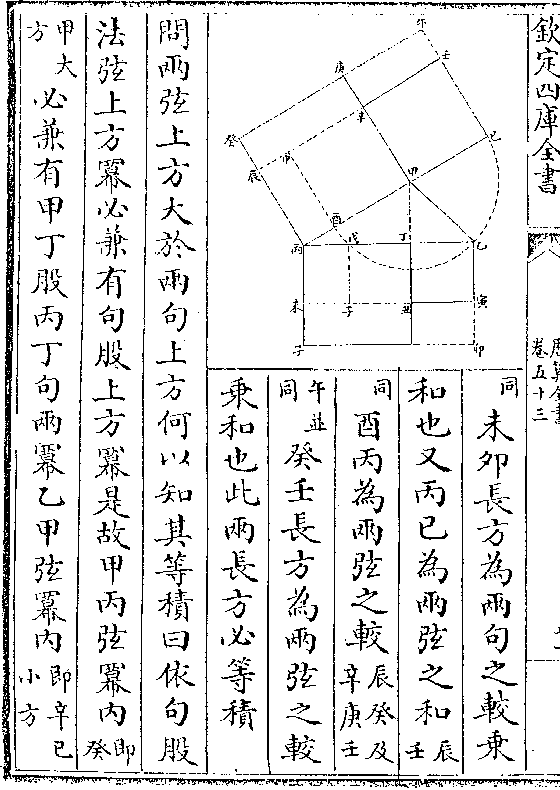一惟亢壁室氐直　形因平视而得正形其壁卯棱线
则成壁氐而斜界于对角分直方形为两句股形矣又
其分截之三方直形亦以平视得正形亦各以棱线分
为两句股而大小相叠成相似之形而比例等矣
　　　　　　　　　　如图亢氐室壁长方以壁氐
　　　　　　　　　　线成两句股而张井辛丙长
　　　　　　　　　　方(即张氐/辛丙)亦以丙卯线(即丙/井亦)
　　　　　　　　　　(即丙/氐)成两句股并形相似则

亢壁与张丙若亢氐与张井(张井即/张氐)
又癸己亥斗长方(即癸氐/亥斗)以斗卯线(即斗己又/即斗氐)成两句
股而房庚甲子长方(即房氐/甲子)亦以子卯线(即子庚又/即子氐)成
两句股而形相似则癸斗与房子若癸己与房庚(癸己/与房)
(庚即癸氐/与房氐)
　
　
　

展形(展之成四句股/面一方直底)　　　合形(合之则成/句股方锥)

　作方直仪法(即句股/立方锥)
法以坚楮依黄赤大距二十三度半画成立面再任设
赤道距至度画成平面再依法画距纬斜立面及黄道
距至度斜平面并方直底然后依棱摺辏即浑员上各
线相为比例之故了然共见
任指黄道或赤道之距至一弧为式即各弧可知其所
用距至弧或在至前或在至后或冬至或夏至并同一
理

方堑堵内容员堑堵法
先解方堑堵
　　　　　　　　堑堵以正方为底(氐卯丁/乙形)其上有
　　　　　　　　赤道象限(氐乾乙弧乙/春分氐夏至)以长方为
　　　　　　　　斜面(亢卯戊/乙形)其上有黄道象限(癸/巽)
　　　　　　　　(乙弧乙春/分巽夏至)底与而一边相连(卯乙/边为)
　　　　　　　　(底与斜面所同用故相/连乃黄赤道之半径)一边相离
　　　　　　　　(氐丁边在底与赤道平行亢戊边/在斜面故相离其距为亢氐为戊)

(丁皆大距度癸/氐弧之切线)其形似斧
从斜面作戊卯对角线切至底(戊丁卯对/角线于底)分堑堵为两
则赤道为两平分(赤道平分于乾乾乙距春分/乾氐距夏至各得四十五度)而黄道
为不平分(黄道分于巽则巽乙距春分四十七度二十强/九分弱而巽癸距夏至四十二度三十一分)
于是黄道切线(戊/乙)与大距度割线(亢/卯)等而方堑堵之形
以成(亢卯为大距二十三度三十一分半之割线其数/一○九○六五戊乙为黄道四十七度二十九分)
(之切线其数亦一○九○六五两数/既同故能作长方斜面而成堑堵)乃黄道求赤道用
两切线之所赖也(若赤道求黄道/则反用其率)

法曰自黄道四十七度二十九分以前用正切是立面
句股比例(戊丁乙句股比例即亢氐卯或用癸巳/卯皆大句股也其酉未乙则为小句股)
　
　
　
　
　右黄道求赤道为以弦求句
一　赤道半径氐卯　　　大句

二　大距割线亢卯　　　大弦
三　赤道切线未乙(甲乙/赤道)　小句
四　黄道切线酉乙(丙乙/黄道)　小弦
　右赤道转求黄道为以句求弦
自黄道四十七度二十九分以后用馀切是斜平面句
股比例(斜面亢虚卯为大句股癸斗卯为小句股在/平面则为氐危卯大句股己心卯小句股)
一　黄道半径癸卯　小股
二　大距割线亢卯　大股

三　黄道馀切癸斗　小句　(牛乙黄道其/馀弧牛癸)
四　赤道馀切亢虚　大句　(女乙赤道其/馀弧女氐)
　右黄道求赤道为以股求句
一　赤道半径氐卯　　　大股
二　大距馀弦己卯　　　小股
三　赤道馀切危氐(即亢/虚)　大句　(女氐即女乙/赤道之馀)
四　黄道馀切心己(即癸/斗)　小句　(牛癸即牛乙/黄道之馀)
　右以赤道转求黄道亦为以股求句

论曰赤道求黄道用句股于赤道平面即郭太史员容
方直之理但郭法起二至则此所谓馀弧乃郭法之正
弧又郭法只用正弦而此用切线为差别耳
又论曰正切线法亦可用于半象限以上馀切线亦可
用于半象限以下此因方堑堵之底正方则所用切线
至方角而止故各用其所宜(云半象限者主赤道而言/若黄道以四十七度二十)
(九分为断一平一斜/故其比例如弦与句)
又论曰正切线法即句股锥形也馀切线法即句股方

锥也以对角斜线分堑堵为两成此二种锥形遂兼两
法

次解员堑堵
方堑堵内容割浑员之分体以癸牛丙乙黄道为其斜
面之界以氐女甲乙赤道为其底之界而以癸氐大距
弧及牛女丙甲等逐度距弧为其高高之势曲抱如浑
员之分斜面平面皆为平员四之一(其高自癸氐大距/渐杀至春分乙角)
(而合为/一点)
员堑堵者虽亦在方堑堵之内然又在所容割浑员分
体之外与割浑员体同底亦以赤道为界而不同面其

面自乙春分过子过奎至亢其形卯乙短而亢卯长如
割平撱员面四之一其撱员边之距心皆以逐度距纬
(如丙甲/牛女等)之割线所至为其界(如卯子为丙甲距弧割线/卯奎为牛女距弧割线之)
(类/)而以逐度距纬之切线为其高(如子甲为丙甲距弧/切线奎女为牛女距)
(弧切线/之类)
法以赤道为围作员柱置浑员在员柱之内对赤道横
剖之则所剖员柱之平员底即赤道平面也又自夏至
依大距二十三度三十分半之切线为高斜对春秋分

剖至心则黄道半周在所剖之斜面矣
然黄道半周虽在所剖斜面而黄道自为半平员所剖
斜面则为半撱员黄道平员在撱员内两端同而中广
异(两端是二分如乙为平撱同用之点中广是/夏至如黄道癸在撱面亢之内其距为癸亢)此员堑
堵之全体也
于是又从亢癸对卯心直剖到底则成员堑堵之半体
即方堑堵所容也此员堑堵斜面之高俱为其所当距
纬弧之切线浑员上弧三角法以距纬切线与赤道平

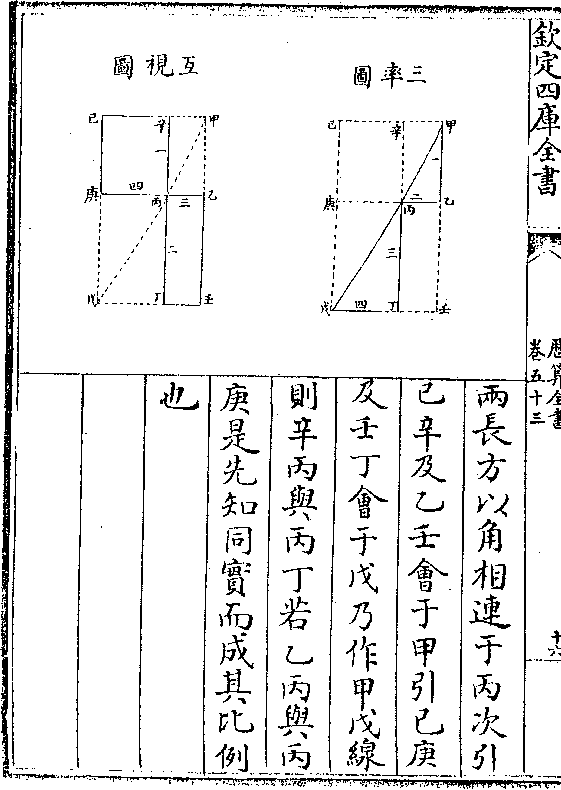面之正弦相连为句股而生比例是此形体中所具之
理
此堑堵体与前图同惟多一亢奎子乙撱弧以此为撱
员界立剖至底令各度俱至赤道而去其外方则成
员堑堵真体
此员堑堵为用子甲丑句股形之所赖子甲为距弧切
线甲丑为赤道正弦也又子甲如股甲丑如句法为子
甲与甲丑若亢氐与氐卯

　
　
　
　
　
　
　
　

　前图为从心视边此为从边视心盖因欲显圆堑堵
　内方直形故为右观之象与前图一理惟多一己庚
　辛乙撱弧(前图亢奎子乙撱弧在黄道斜面/此图己庚辛乙撱弧在赤道平面)
员堑堵有二
若自斜面之黄道象限各度直剖至赤道平面亦成员
堑堵象限然又在剖浑员体分之内其体以斜面为正
象限但斜立耳其底在赤道者转成撱员
此撱员形在赤道象限之内惟乙点相连此即简平仪

之理
其撱之法则以卯乙半径为大径癸氐距弧之馀弦卯
巳为小径小径当二至大径当二分与前法正相反然
其比例等何也割线与全数若全数与馀弦也
此员堑堵以撱形为底象限为斜面以距度逐度之正
弦为其高乃黄道距纬相求用两正弦之所赖也
此员堑堵内又容小方堑堵乃郭太史所用员容方直
也

浑员因斜剖作角而生比例成方员堑堵形其角自○
度一分以至九十度凡五千四百则方员堑堵亦五千
四百矣(乙角以春分为例则其度二十三度半强其实/自一分至九十度并得为乙角合计之则五千)
(四/百)
每一堑堵依度对心剖之成立句股锥及方句股锥之
眠体自○度一分至大距止亦五千四百
以五千四百自乘凡二千九百一十六万而浑员之体
之势乃尽得其比例乌呼至矣

每度分有方堑堵方堑堵内函赤道所生撱体赤道撱
体内又函黄道所生撱体黄道撱体内又函小方堑堵每
度分有此四者则一象限内为五千四百者四共二万
一千六百(以乙角五四○○乘之则/一一六六四○○○○)
每度有正有馀对心斜分则正度成句股锥馀度成方
底句股锥之眠体一象限凡四万三千二百(以五四○/○乘之则)
(二三三二八/○○○○)

员容方直简法序
古未有预立算数以尽句股之变者有之自西洋八线
表始古未有作为仪器以写浑员内句股之形者自愚
所撰立三角始立三角之仪分之曰句股锥形曰句股
方锥形合之则成堑堵形其称名也小其取类也大径
寸之物以状浑员而弧三角之理如指诸掌即古法之
通于弧三角者亦如指诸掌矣虽然犹无解于古法之
不用割切也故复作此简法以互徵之而授时历三图

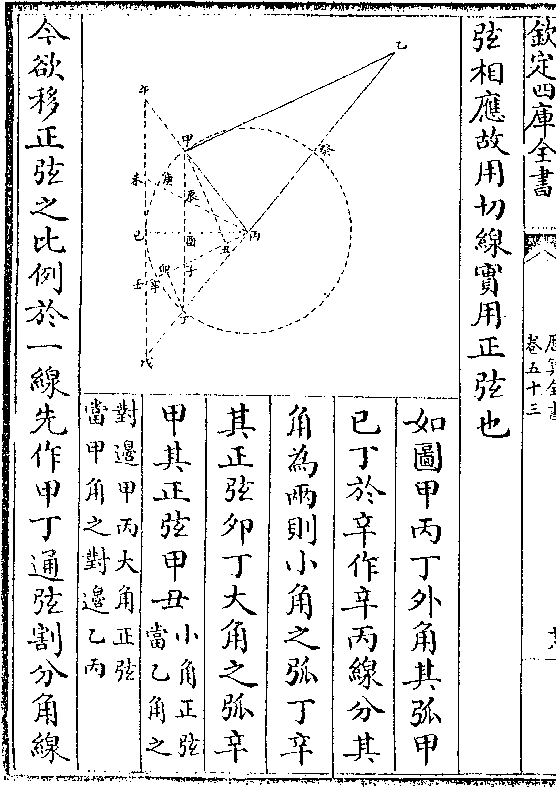附焉盖理得数而彰数得图而显图得器而真草野无
诸仪象藉兹以自释其疑不敢自私故以公之同好云
尔(句股锥形是以西法通国法句鈠方锥形是以郭法/通西法今此简法是专解郭法而两法相同之故自)
(具其/中)

员容方直仪简法(即句股方锥之方直仪而不用割切/线祗以各弧正弦矢度相求其用己)
(足亦不/须用角)
　
　
　
　
　
立面中有句股形二其一大句股形(癸巳/乙)以黄道半径

(癸/乙)为弦大距度正弦(癸/巳)为股大距度馀弦(巳/乙)为句其一
小句股形(壬戊/乙)以黄道馀弦(壬/乙)为弦距纬正弦(壬/戊)为股
楞线(戊/乙)为句

平面中亦有句股形二其一小句股形(庚戊/乙)以距纬丙
甲之馀弦(庚/乙)为弦以黄道正弦(戊/庚)为股楞线(戊/乙)为句其
一大句股形(甲辛/乙)以赤道半径(甲/乙)为弦以赤道正弦(甲/辛)
为股赤道馀弦(辛/乙)为句(戊乙线于弧度无取然平立二/形并得此补成句股谓之楞线)
　　　　黄道正弦本在斜平面而能移于平面者有
　　　　相望两立线(丙庚/壬戊)为之限也距度正弦本在
　　　　斜立面而能移于立面者有上下两横线(丙/壬)
　　　　(庚/戊)为之限也此四线(两立/两横)相得成长方其立

如堵故又曰弧容直阔也

有大距有黄道而求距纬　更之可求大距　反之可求黄道
　一　半径　　　癸乙　一　黄道馀弦　一　大距正弦
　二　大距正弦　癸己　二　距纬正弦　二　半径
　三　黄道馀弦　壬乙　三　半径　　　三　距纬正弦
　四　距纬正弦　壬戊　四　大距正弦　四　黄道馀弦
有赤道有距纬而求黄道　更之可求赤道　反之可求距纬
　一　半径　　　甲乙　一　距纬馀弦　一　赤道正弦
　二　赤道正弦　甲辛　二　黄道正弦　二　半径

　三　距纬馀弦　庚乙　三　半径　　　三　黄道正弦
　四　黄道正弦　庚戊　四　赤道正弦　四　距纬馀弦

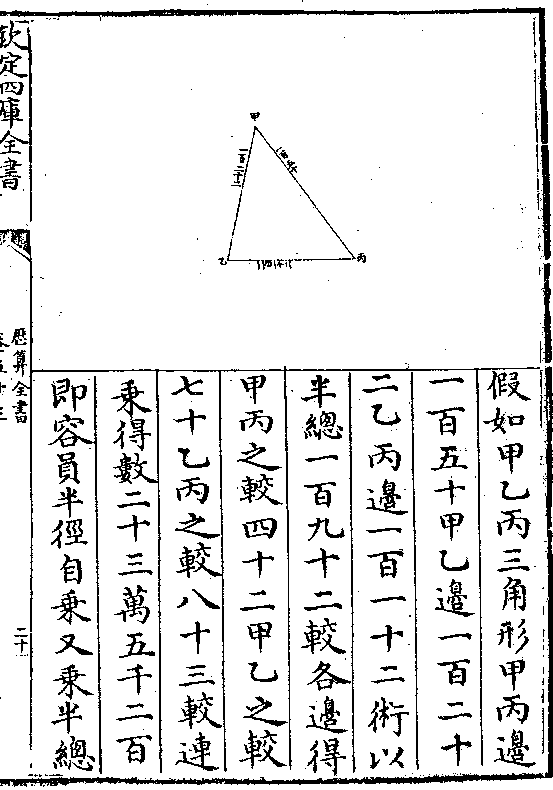郭太史本法
弧矢割员图(见授时历/草下并同)
　　　　　　　　　　凡浑员中割成平员任割平
　　　　　　　　　　员之一分成弧矢形皆有弧
　　　　　　　　　　背有弧弦有矢割弧背之形
　　　　　　　　　　而半之则有半弧背有半弧
　　　　　　　　　　弦有矢　因弧矢生句股形
　　　　　　　　　　以半弧弦为句(即正/弦)矢减半

径之馀为股(即馀/弦)半径则常为弦　句股内又成小句
股则有小句小股小弦而大小可以互求或立或平可
以互用(平视侧视二/图皆从此出)

侧视之图
　　　　　　　　　　横者为赤道(赤道一规因旁/视如一直线黄)
　　　　　　　　　　(道/同)
　　　　　　　　　　斜者为黄道
　　　　　　　　　　因二至黄赤之距成大句股
　　　　　　　　　　(即外/圈)
　　　　　　　　　　因各度黄赤之距成小句股
　

平视之图
　　　　　　　　　　外大员为赤道
　　　　　　　　　　内撱者黄道(从两极平视则/黄道在赤道内)
　　　　　　　　　　(而成/撱形)
　　　　　　　　　　有赤道各度即各其有半弧
　　　　　　　　　　弦以生大句股
　　　　　　　　　　又各有其相当之黄道半弧
　　　　　　　　　　弦以生小句股(此二者皆/可互求)

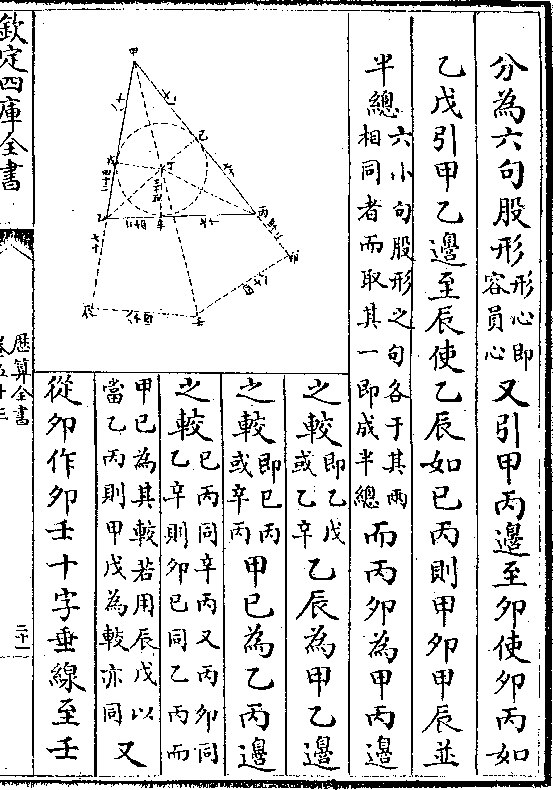授时历求黄赤内外度及黄赤道差法
置黄道矢(本法用带从三/乘方求各度矢)去减周天半径(即立面黄/道半径)馀
为黄赤道小弦(即黄道馀弦也半径/为大弦故此为小弦)置黄赤道小弦以
二至内外半弧弦(即二至大距度正弦当时/实测为二十三度九十分)乘之为实
黄赤大弦(即周天半径以其为立面/大句股之弦故称大弦)为法除之得黄赤
道内外半弧弦(即各度黄赤距度正弦也原法以矢度/度半背弦差加入半弧弦得内外半弧)
(背今/省)
又置黄赤道小弦以黄赤道大股(即二至内外度馀弦/也在立面大句股形)

(为大/股)乘之为实黄赤道大弦为法除之(解见/前)得黄赤道
小股(即立面平面两小句股同用之楞/线在立面与大股相比故称小股)置黄道半弧弦
(即黄道正弦也原法以黄道矢/求半背弦差减黄道度得之)自乘为股幂黄赤小股
自乘为句幂(即楞线也先在立面为小句股形之股今/又为平面句股形之句故其幂称句幂)
两幂并之为实开平方法除之为赤道小弦(即各度黄/赤距度馀)
(弦也周天半径为平面上大句股之弦/故称大弦则此为小句股弦当称小弦)置黄道半弧弦
以周天半径乘之为实赤道小弦为法除之得赤道半
弧弦(即赤道正弦也原法求半背弦/差以加半弧弦得赤道今省)

论曰弧矢割员者平员法也以测浑员则有四用一曰
立弧矢势如张弓以量黄赤道二至内外度即侧立图
也一曰平弧矢形如伏弩以量赤道即平视图也一曰
斜弧矢与平弧矢同法而平面边高边下其庋起处如
二至内外之度以量黄道即平视图中小句股也一曰
斜立弧矢与立弧矢同法而其立稍偏以量黄赤道各
度之内外度即侧立图中小句股也自离二至一度起
至近二分一度止一象限中逐度皆有之但皆小于二

至之距邢台郭太史弧矢平立三图中具此四法即弧
三角之理无不可通言简而意尽包举无穷好古者所
当宝爱而?玩也
又论曰割员之算始于魏刘徽至刘宋祖冲之父子尤
精其术唐宋以算学设科古书犹未尽亡邢台盖有所
本厥后授时历承用三百馀年未加修改测箕之讲求
益稀学士大夫既视为不急之务而台官株守成法鲜
谙厥故骤见西术群相骇诧而不知旧法中理本相同

也畴人子弟多不能自读其书又忌人之读而各私其
本久之而书亦不可问矣考元史历成之后所进之书
凡百有馀卷(郭守敬传有修改源流及测验等书齐履/谦传有经串演撰诸书明历法之所以然)
今其存轶并不可考良可浩叹然天下之人岂无有能
藏弆遗文以待后学者庶几出以相證予于斯图之义
类多通而深有望于同志矣
问元初有回回历法与今西法大同小异邢台盖会通
其说而为之故其法相通若是与曰九章句股作于𨽻

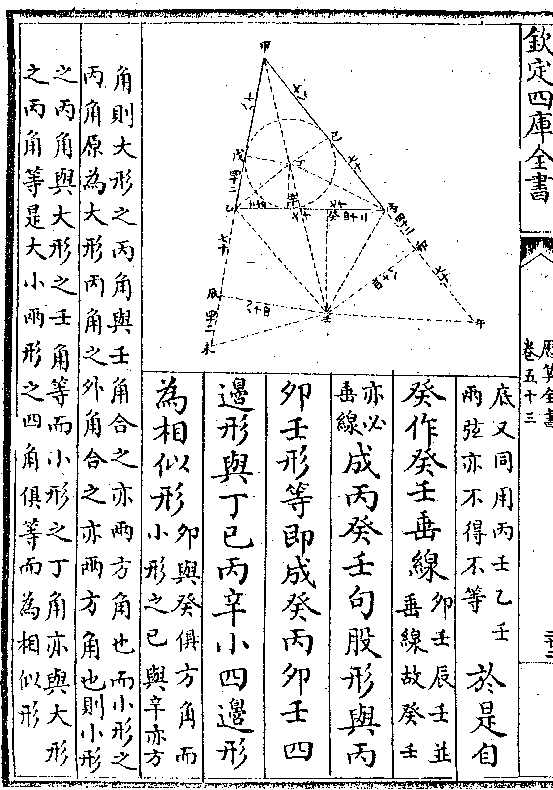首为测量之根本三代以上学有专家大司徒以三物
教民而数居六艺之一秦火以后吾中土失之而彼反
存之至于流远𣲖分遂以各名其学而不知其本之同
也况东西共戴一天即同此句股测员之法当其心思
所极与理相符虽在数万里不容不合亦其必然者矣
考元初有西域人进万年历未经试用迨明洪武年间
始命词臣吴伯宗西域大师马沙亦黑等译回回历书
三卷然亦粗具算法立成并不言立法之原究竟不知

其所用何法或即今三角八线或更有他法俱无可考
虽其子孙莫能言之考元史所载西域人晷影堂诸制
与郭法所用简仪高表诸器无一同者或测量之理触
类增智容当有之然未见其有会通之处也徐文定公
言回回历纬度凌犯稍为详密然无片言只字言其立
法之故使后来入室无因更张无术盖以此也又据历
书言新法之善系近数十年中所造则亦非元初之西
法矣而与郭图之理反有相通岂非论其传各有本末

而精求其理本无异同耶且郭法用员容方直起算冬
至西法用三角起算春分郭用三乘方以先得矢西用
八线故先得弦又西专用角而郭只用弧西兼用割切
而郭只用弦种种各别而不害其同有所以同者在耳
且夫数者所以合理也历者所以顺天也法有可采何
论东西理所当明何分新旧在善学者知其所以异又
知其所以同去中西之见以平心观理则弧三角之详
明郭图之简括皆足以资探索而启深思务集众长以

观其会通毋拘名相而取其精粹其于古圣人创法流
传之意庶几无负而羲和之学无难再见于今日矣

角即弧解
问古法只用弧而西法用角有以异乎曰角之度在弧
　　　　　故用角实用弧也何以明其然也假如辰
　　　　　庚己三角形有庚钝角有己庚辰庚二边
　　　　　欲求诸数依垂弧法于不知之辰角打线
　　　　　线先补求辰辛及辛庚成辰辛庚三角虚
　　　　　形此必用庚角以求之而庚角之度为丙
　　　　　丁是用庚角者实用丙丁也其法庚丙九

十度之正弦(即半/径)与丙丁弧之正弧(即庚角/正弦)若庚辰正
弦与辰辛正弦是以大句股之例例小句股也又丙丁
弧之割线(即庚角/割线)与庚丁九十度之正弦(亦即半径凡/角度所当弧)
(其两边并/九十度)若庚辰之切线与庚辛之切线亦是以大句
股之例例小句股也
既补成辰辛巳三角形可求巳角而巳角之度为乙甲
是求巳角者实求乙甲也其法辛己弧之正弦与辰辛
弧之切线若己甲象弧之正弦(即半/径)与乙甲弧之切线

(即己角/切线)是以小句股例大句股也
又如己辰庚形庚为锐角当自不知之辰角打线分为
　　　　　二形以求诸数其一辰辛庚分形先用庚
　　　　　角而庚角之度为丙丁用庚角实用丙丁
　　　　　也法为丙庚象弧之正弦(即半/径)于丙丁弧
　　　　　之正弦(即庚角/正弦)若辰庚之正弦与辰辛之
正弦又丙庚象弧之正弧(即半/径)与丙丁弧之馀弦(即庚/角馀)
(弦/)若辰庚之切线与辛庚之切线是以大句股例小句

股也
其一辰辛己分形(以庚辛减己/庚得己辛)有辰辛己辛二边可求
己角而己角之度为乙甲求己角实求乙甲也法为己
辛之正弦与辰辛之切线若己甲象弧之正弦(即半/径)与
乙甲弧之切线(即己角/切线)是以小句股例大句股也
一系　用角求弧是以大句股比例比小句股用弧求
角是以小句股比例比大句股
　历算全书卷六十