声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
卷一 第 1a 页 WYG0799-0003c.png
 钦定四库全书
钦定四库全书御制数理精蕴上编卷一
数理本原
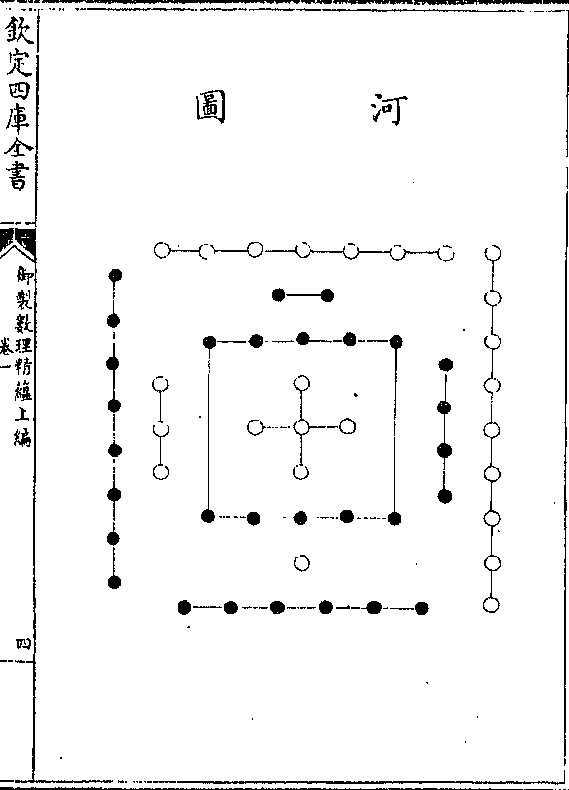
河图
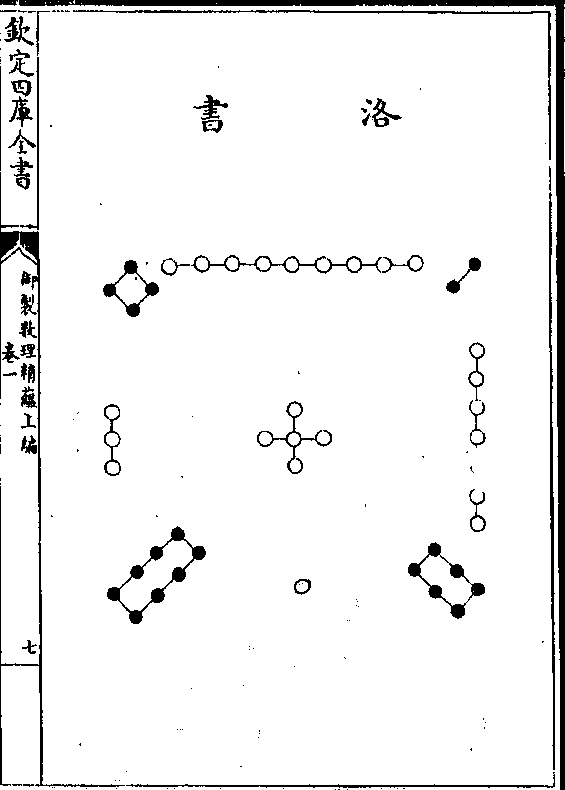
洛书
周髀经解
卷一 第 2a 页 WYG0799-0004a.png
 数理本原
数理本原粤稽上古河出图洛出书八卦是生九畴是叙数学
亦于是乎肇焉盖图书应天地之瑞因圣人而始出
数学穷万物之理自圣人而得明也昔黄帝命𨽻首
作算九章之义已启尧命羲和治历敬授人时而岁
功已成周官以六艺教士数居其一周髀商高之说
可考也秦汉而后代不乏人如洛下闳张衡刘焯祖
冲之之徒各有著述唐宋设明经算学科其书颁在
卷一 第 2b 页 WYG0799-0004b.png WYG0799-0004c.png

 学宫令博士弟子肄习是知算数之学实格物致知
学宫令博士弟子肄习是知算数之学实格物致知之要务也故论其数设为几何之分而立相求之法
加减乘除凡多寡轻重贵贱盈朒无遗数也论其理
设为几何之形而明所以立算之故比例分合凡方
圆大小远近高深无遗理也溯其本原加减实出于
河图乘除殆出于洛书一奇一偶对待相资递加递
减而繁衍不穷焉奇偶各分纵横相配互乘互除而
变通不滞焉徵其实用测天地之高深审日月之交
会察四时之节候较昼夜之短长以至协律度同量
卷一 第 2b 页 WYG0799-0004b.png WYG0799-0004c.png

 衡通食货便营作皆赖之以为统纪焉今汇集成编
衡通食货便营作皆赖之以为统纪焉今汇集成编卷一 第 3a 页 WYG0799-0005a.png
 以类相从提点线面体以为纲分和较顺逆以为目
以类相从提点线面体以为纲分和较顺逆以为目法无论巨细惟择其善者由浅以及深执简以御繁
使理与数协务有裨于天下国家以传于亿万世云
尔
卷一 第 4a 页 WYG0799-0005c.png

卷一 第 4b 页 WYG0799-0005d.png
 易系辞曰天一地二天三地四天五地六天七地八
易系辞曰天一地二天三地四天五地六天七地八天九地十天数五地数五五位相得而各有合朱子
曰河图以五生数统五成数而同处其方盖揭其全
以示人而道其常数之体也考其数始于一中于五
终于十阳奇阴偶而数之加减由是生焉自一而二
自二而三自三而四自四而五皆递加一以相生自
五复加一而成六六加一而七七加一而八八加一
而九九加一而十十则仍归于一故至十而天地之
数全矣天数阳也地数阴也言天地即所以言阴阳
卷一 第 5a 页 WYG0799-0006a.png
 也五位相得而各有合以五行之序而定位也邵子
也五位相得而各有合以五行之序而定位也邵子曰天之阳在南而阴在北地之阴在南而阳在北故
河图之数一阳位于北二阴位于南其即五行质具
于地之义而言之欤今以阴阳相生之数论之一为
阳天一生水而位北一加一为二为阴地二生火而
位南二加一为三为阳天三生木而位东三加一为
四为阴地四生金而位西四加一为五为阳天五生
土而位中至五而五行之数已周此生数之极也自
卷一 第 5b 页 WYG0799-0006b.png WYG0799-0006c.png

 一至五则五又为一体矣于是以五为中数而复加
一至五则五又为一体矣于是以五为中数而复加一则为六六阴也因五中数与一相加故与一同位
而属之水焉六加一为七以中数五计之实加二故
与二同位而属之火焉七加一为八以中数五计之
实加三故与三同位而属之木焉八加一为九以中
数五计之实加四故与四同位而属之金焉九加一
为十以中数五计之复加五故与五同位而属之土
焉至十而五行之数再周天地之数已备此成数之
极也以阴阳运行之序论之以五生数统十成数位
卷一 第 5b 页 WYG0799-0006b.png WYG0799-0006c.png

 居于中而奇数则始于北一次东三次南七次西九
居于中而奇数则始于北一次东三次南七次西九卷一 第 6a 页 WYG0799-0007a.png
 偶数则始于南二次西四次北六次东八此数之阴
偶数则始于南二次西四次北六次东八此数之阴与阴阳与阳各从其类者也以奇偶相得之数论之
一与六合二与七合三与八合四与九合五与十合
此又奇偶相得而各有合者也邵子谓圆者河图之
数又曰历纪之数其肇于此然则所谓数者即一阴
一阳一奇一偶循环无间表里相维百千万亿总由
此推之以成其变化河图者岂非天地自然生成之
数也哉
卷一 第 7a 页 WYG0799-0007c.png

卷一 第 7b 页 WYG0799-0007d.png
 洛书之数戴九履一左三右七二四为肩八六为足
洛书之数戴九履一左三右七二四为肩八六为足五居其中朱子谓以五奇数统四偶数而各居其所
盖主于阳以统阴而肇其变数之用也邵子曰数学
虽多乘除尽之矣夫洛书者数之源也乘除之所以
生也易说卦传曰参天两地而倚数三天数也二地
数也天地相合而万物育焉一者太极之体其数不
行故数行于二三起于三以三参之则三九七一之
数生焉起于二以二两之则二四八六之数生焉其
序列之位则天居四正取以阳统阴之义地居四维
卷一 第 8a 页 WYG0799-0008a.png
 取以阴从阳之义其三九七一乘数则旋而左除数
取以阴从阳之义其三九七一乘数则旋而左除数则返而右也其二四八六乘数则旋而右除数则返
而左也二三相合而为五五则无对居中者立其体
也二五相合而为十十仍归一洛书不用者藏其用
也是故三始于东方发生之地而位于左自东而南
三而三之是为九故戴九自南而西九而三之为二
十七去成数馀七故右七自西而北七而三之为二
十一去成数馀一故履一奇数左旋以三参之即天
卷一 第 8b 页 WYG0799-0008b.png WYG0799-0008c.png

 道左行之说也如转而右行以三除之仍复其原数
道左行之说也如转而右行以三除之仍复其原数焉二立于西南二阴始生之地而位于右肩自西南
而东南二而二之是为四位于左肩自东南而东北
四而二之为八位于左足自东北而西北八而二之
为十六去十馀六位于右足偶数右旋以二两之即
地道右行之说也如转而左行以二除之仍复其原
数焉此乘除之数见于运行者如此若以对待者观
之一与九对一为数之始九为数之终互乘互除其
数不变也二与八对二八互乘俱得十六二除十六
卷一 第 8b 页 WYG0799-0008b.png WYG0799-0008c.png

 得八八除十六仍得二此二与八之相倚也三与七
得八八除十六仍得二此二与八之相倚也三与七卷一 第 9a 页 WYG0799-0009a.png
 对三七互乘皆二十一三除二十一得七七除二十
对三七互乘皆二十一三除二十一得七七除二十一仍得三此三与七之相倚也四与六对四六互乘
皆二十四四除二十四得六六除二十四仍得四此
四与六之相倚也至五为二三之合天地之交阴阳
之会位于洛书之中以建人极配上下而为三才故
斜直四围皆得十五合之得四十有五为九五之数
要之运行者其序也对待者其位也进退循环纵横
交错总不外于乘除故曰乘除之本原自洛书生也
卷一 第 10a 页 WYG0799-0009c.png
 周髀经解
周髀经解数学之失传久矣汉晋以来所存几如一线其后
祖冲之郭守敬辈殚心象数立密率消长之法以
为习算入门之规然其法以有尽度无尽止言天
行未及地体是以测之有变更度之多盈缩盖有
未尽之馀蕴也明万历间西洋人始入中土其中
一二习算数者如利玛窦穆尼阁等著为几何原
本同文算指诸书大体虽具实未阐明理数之精
卷一 第 10b 页 WYG0799-0009d.png WYG0799-0010a.png
 微及我朝定鼎以来远人慕化至者渐多有汤若
微及我朝定鼎以来远人慕化至者渐多有汤若望南怀仁安多闵明我相继治理历法间明算学
而度数之理渐加详备然询其所自皆云本中土
所流传粤稽古圣尧之钦明舜之浚哲历象授时
闰馀定岁璿玑玉衡以齐七政推步之学孰大于
是至于三代盛时声教四讫重译向风则书籍流
传于海外者殆不一矣周末畴人子弟失官分散
嗣经秦火中原之典章既多缺佚而海外之支流
反得真传此西学之所以有本也古算书存者独
卷一 第 10b 页 WYG0799-0009d.png WYG0799-0010a.png

 有周髀周公商高问答其本文也荣方陈子以下
有周髀周公商高问答其本文也荣方陈子以下卷一 第 11a 页 WYG0799-0010c.png
 所推衍也而汉张衡蔡邕以为术数虽存考验天
所推衍也而汉张衡蔡邕以为术数虽存考验天状多所违失按荣方陈子始言晷度衡邕所疑或
在于是若周髀本文辞简而意该理精而用博实
言数者所不能外其圆方矩度之规推测分合之
用莫不与西法相为表里然则商高一篇诚成周
六艺之遗文而非后人所能假托也旧注义多舛
讹今悉详正弁于算书之首以明数学之宗使学
者知中外本无二理焉尔
卷一 第 11b 页 WYG0799-0010d.png WYG0799-0011a.png

 昔者周公问于商高曰窃闻乎大夫善数也请问古
昔者周公问于商高曰窃闻乎大夫善数也请问古者包牺立周天历度
周天历度者分周天三百六十度为推求历日之
用也按通鉴载包牺作甲历天干地支相配六甲
一转天度一周年以是纪而岁功成月以是纪而
朔望定昼夜以是纪而时日分易大传言包牺仰
以观于天文俯以察于地理其观察之时必有度
数以纪其法象则历度始于包牺无疑矣
夫天不可阶而升地不可将尺寸而度请问数从安
卷一 第 11b 页 WYG0799-0010d.png WYG0799-0011a.png

 出
出卷一 第 12a 页 WYG0799-0011c.png
 天之高明地之博厚非人力所能及其历度之数
天之高明地之博厚非人力所能及其历度之数不知从何而得也
商高曰数之法出于圆方
万物之象不出圆方万象之数不离圆方河图者
方之象也洛书者圆之象也太极者圆之体奇也
四象者方之体偶也奇数天也偶数地也有天地
而万物于是乎生有圆方而万象于是乎定有奇
偶而万数于是乎立矣
卷一 第 12b 页 WYG0799-0011d.png WYG0799-0012a.png

 圆出于方
圆出于方以数而论出于圆方以圆方而论则圆出于方盖
方易度而圆难测方有尽而圆
无尽故推圆者以方度之以有
尽而度无尽也是以圆周内弦
外切屡求勾股为无数多边形
以切近圆界将合而为一而圆
周始得故曰圆出于方也
方出于矩
卷一 第 12b 页 WYG0799-0011d.png WYG0799-0012a.png

 孟子曰不以规矩不能成方圆夫规所以成圆而
孟子曰不以规矩不能成方圆夫规所以成圆而卷一 第 13a 页 WYG0799-0012c.png
 矩所以成方也故凡方形必出
矩所以成方也故凡方形必出于二矩相合如矩之二股均者
合之即为正方矩之二股一大
一小者合之则为长方盖因矩
之为形其角直其线正所以能
成方体此又直内方外之理故曰方出于矩也
矩出于九九八十一
度圆方者递归于矩而矩之形总不外乎二数相
卷一 第 13b 页 WYG0799-0012d.png WYG0799-0013a.png

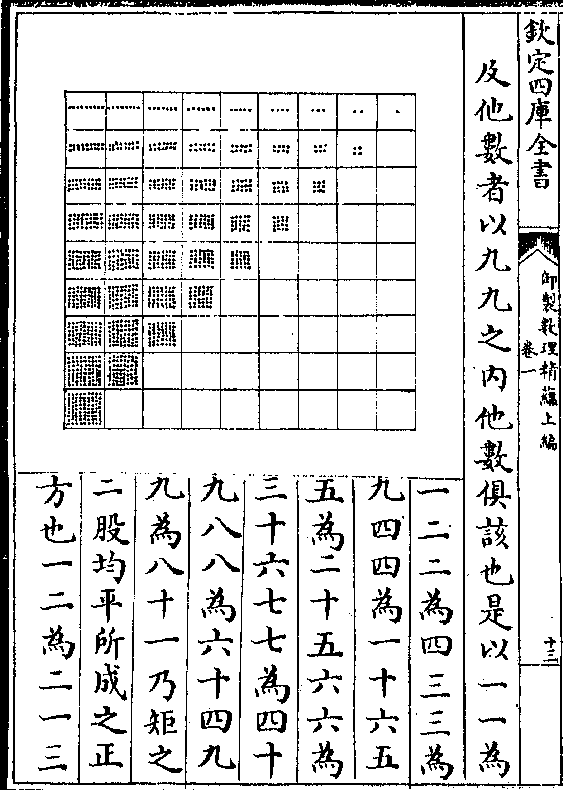
 乘九九者数之终而一一乃数之始言九九而不
乘九九者数之终而一一乃数之始言九九而不及他数者以九九之内他数俱该也是以一一为
一二二为四三三为
九四四为一十六五
五为二十五六六为
三十六七七为四十
九八八为六十四九
九为八十一乃矩之
二股均平所成之正
卷一 第 13b 页 WYG0799-0012d.png WYG0799-0013a.png

 方也一二为二一三
方也一二为二一三卷一 第 14a 页 WYG0799-0013c.png
 为三一四为四一五为五一六为六一七为七一
为三一四为四一五为五一六为六一七为七一八为八一九为九形虽未方而其理犹存也二三
为六二四为八二五一十二六一十二二七一十
四二八一十六二九一十八三四一十二三五一
十五三六一十八三七二十一三八二十四三九
二十七四五二十四六二十四四七二十八四八
三十二四九三十六五六三十五七三十五五八
四十五九四十五六七四十二六八四十八六九
卷一 第 14b 页 WYG0799-0013d.png WYG0799-0014a.png

 五十四七八五十六七九六十三八九七十二乃
五十四七八五十六七九六十三八九七十二乃矩之一股小一股大所成之长方也至于一百之
类虽为正方乃十之相乘十则仍归于一也又如
八十四九十六之类乃六七四十二六八四十八
之倍不得自立为数之本又或十一十三十七十
九之类十一为二五一十之奇十三为二六一十
二之奇十七为四四一十六之奇不得成正方亦
不得成长方故不入九九之数也是以九九之数
为方之本而方之形必合以矩故曰矩出于九九
卷一 第 14b 页 WYG0799-0013d.png WYG0799-0014a.png

 八十一也
八十一也卷一 第 15a 页 WYG0799-0014c.png
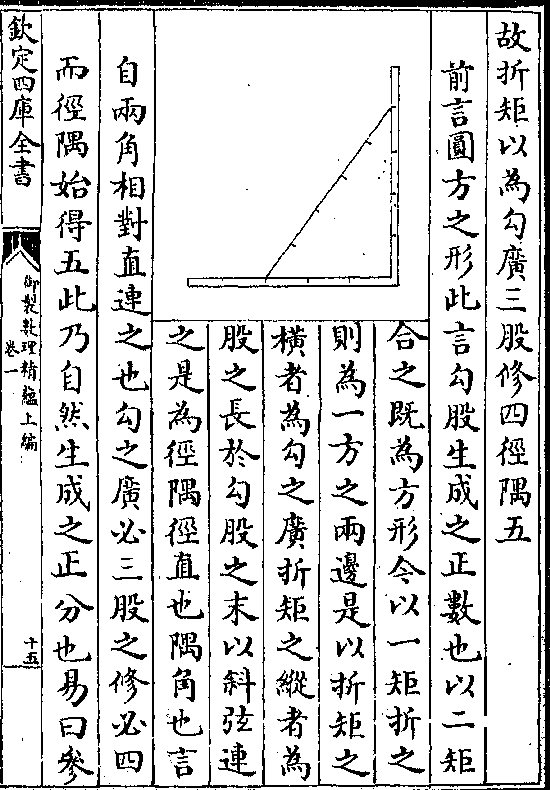
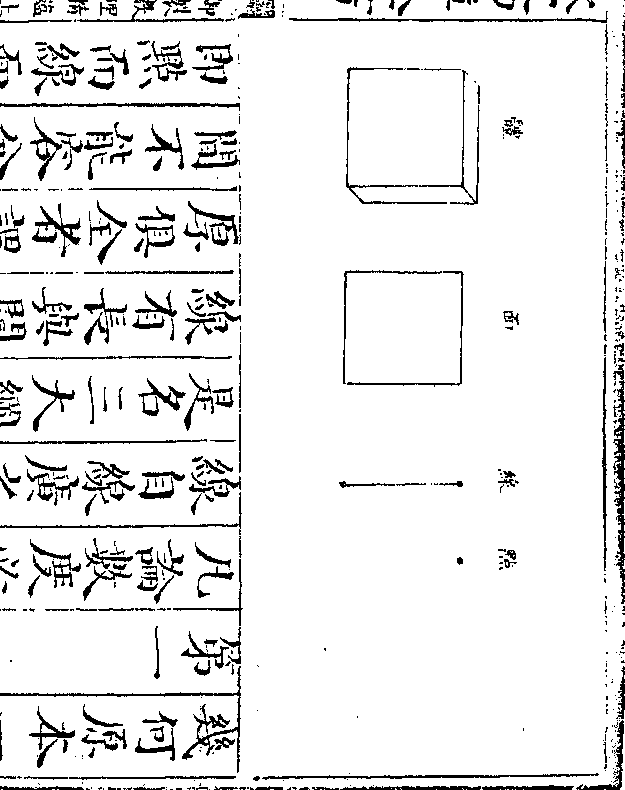 故折矩以为勾广三股修四径隅五
故折矩以为勾广三股修四径隅五前言圆方之形此言勾股生成之正数也以二矩
合之既为方形今以一矩折之
则为一方之两边是以折矩之
横者为勾之广折矩之纵者为
股之长于勾股之末以科弦连
之是为径隅径直也隅角也言
自两角相对直连之也勾之广必三股之修必四
卷一 第 15b 页 WYG0799-0014d.png WYG0799-0015a.png

 而径隅始得五此乃自然生成之正分也易曰参
而径隅始得五此乃自然生成之正分也易曰参天两地而倚数天数一参之则为三地数二两之
则为四三二合之则为五此又勾三股四弦五之
正义也
既方其外半其一矩
此言勾股之面积也勾股以弦连之不得为方形
必再合一矩乃为一长方所谓方其外者言弦之
外复加一矩以成方也勾三股四相乘得一十有
二即为两矩合成之数半之得六乃勾股之面积
卷一 第 15b 页 WYG0799-0014d.png WYG0799-0015a.png

 所谓半其一矩者也
所谓半其一矩者也卷一 第 16a 页 WYG0799-0015c.png
 环而共盘得成三四五
环而共盘得成三四五此言勾股弦相和之数也环而共盘者环绕盘旋
于勾股弦之周围得成三四五共之为一十有二
乃三数相和之总数也
两矩共长二十有五是为积矩
此言勾股相求之法也两矩者勾与股也其所以
相求者以勾股弦各面积彼此加减以立法也勾
三自乘为九股四自乘为一十有六合而计之为
卷一 第 16b 页 WYG0799-0015d.png WYG0799-0016a.png

 二十有五是勾股各自乘之积相并而与弦自乘
二十有五是勾股各自乘之积相并而与弦自乘之积等故曰积矩也弦之自乘
积内减勾自乘之积得股自乘
之积弦之自乘积内减股自乘
之积得勾自乘之积故为勾股
弦相求之法也
故禹之所以治天下者此数之所由生也
言禹之平成之功昭垂万古揆厥所以奏绩者必
藉勾股以审高下始得顺水之性而告厥成功也
卷一 第 16b 页 WYG0799-0015d.png WYG0799-0016a.png

 然则禹之所以治水者非此勾股之数所由生乎
然则禹之所以治水者非此勾股之数所由生乎卷一 第 17a 页 WYG0799-0016c.png
 周公曰大哉言数请问用矩之道
周公曰大哉言数请问用矩之道商高曰平矩以正绳
此言用矩立法必以正且直也平矩以正绳有两
义平置其矩使矩之角直以此直角之一股或横
或平(横以度远/平以度高)复自一股引绳以度其分则此分
为我所知故以所知推所不知此绳引长时必使
与直角对正不论其分之几何引之亦必令直方
能得测度之准故为平矩以正绳又平者均平整
卷一 第 17b 页 WYG0799-0016d.png WYG0799-0017a.png

 齐之谓用矩之道矩之角正(即直角/之说也)然后二股得
齐之谓用矩之道矩之角正(即直角/之说也)然后二股得直以之测高测远乃得度其大小之分此矩既正
而所测之度亦正矣孟子曰规矩准绳以为方圆
平直绳者即准之之意规矩所以度圆方而准绳
所以考平直故准之以平绳之以直始得立法之
精微故曰平矩以正绳也
偃矩以望高
此用矩测高之法也偃者仰也仰矩方可测高矩
之一股植立在前一股定平在下然后比例推之
卷一 第 17b 页 WYG0799-0016d.png WYG0799-0017a.png

 盖平股与立股之比即所知之远与所测之高之
盖平股与立股之比即所知之远与所测之高之卷一 第 18a 页 WYG0799-0017c.png
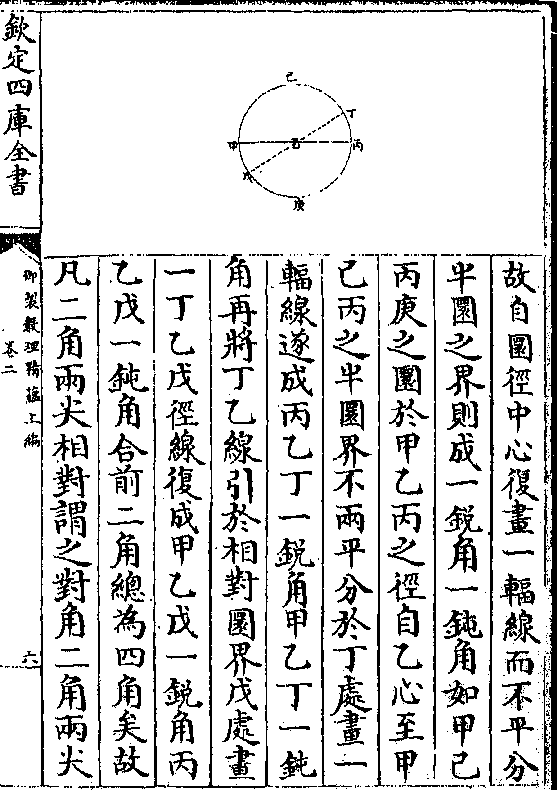 比也故仰测之而得高
比也故仰测之而得高覆矩以测深
此用矩测深之法也覆者俯也俯矩方可测深矩
之一股立者在前一股平者在上平股与立股之
比即所知之远与所测之深之比也故俯测之而
得深
卧矩以知远
此用矩测远之法也卧者平也平矩方可测远以
卷一 第 18b 页 WYG0799-0017d.png WYG0799-0018a.png

 矩之一股为横向内一股为纵向前是以横与纵
矩之一股为横向内一股为纵向前是以横与纵之比即所知之度与所求之远之比也故平测之
而得远
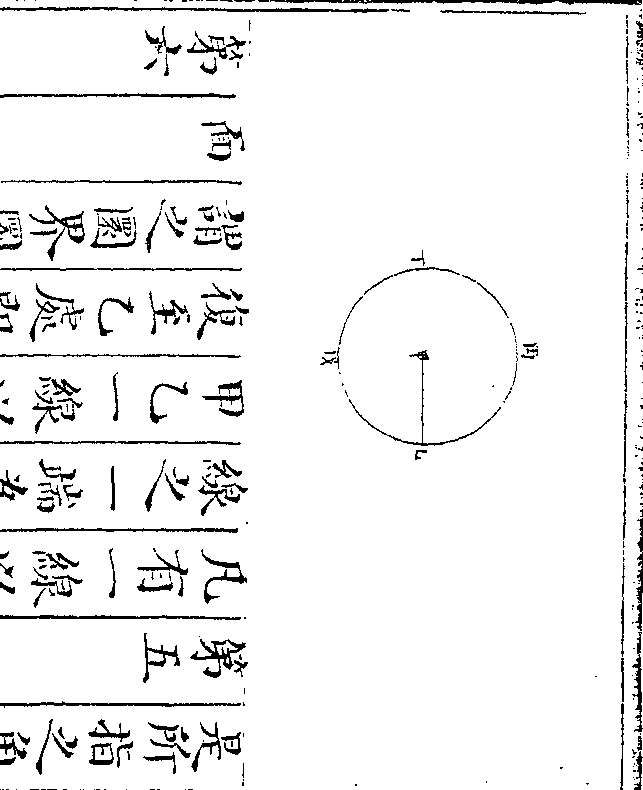
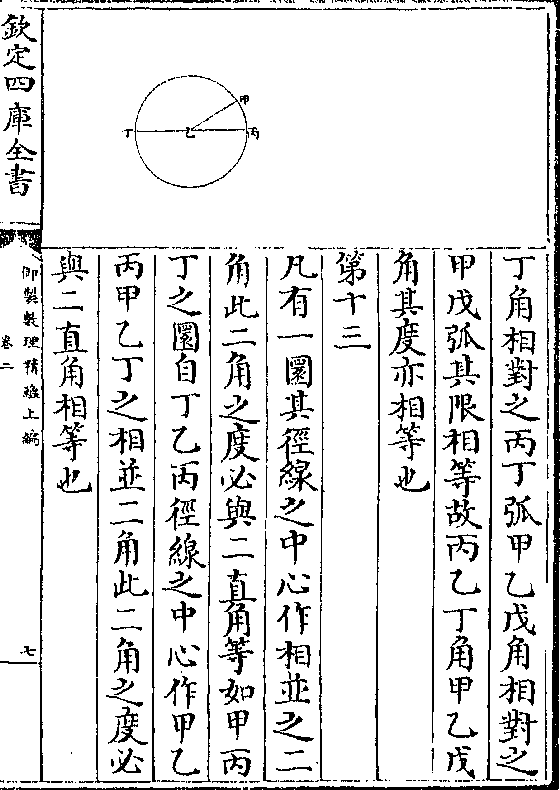
环矩以为圆
此用矩为圆之法也以矩之一端为枢一端旋转
为圆则成一圜环矩者即旋规之说也
合矩以为方
此用矩为方之法也矩二股也两矩相合乃成一
方即前方出于矩之说也
卷一 第 18b 页 WYG0799-0017d.png WYG0799-0018a.png

 方属地圆属天天圆地方
方属地圆属天天圆地方卷一 第 19a 页 WYG0799-0018c.png
 前言用矩以测高深广远复用矩以为圆方此以
前言用矩以测高深广远复用矩以为圆方此以圆方属之天地者非以形体言盖以阴阳动静之
理言也乐记云著不息者天也著不动者地也不
息故运而不积圆之象也不动故静而有常方之
理也且圆之数无尽而方之数有尽天不可阶而
升测天者恒于地上度之是仍以方度圆也凡数
之不尽者必奇数之可尽者必偶是以阳为奇阴
为偶此方圆之理数所以属乎天地也
卷一 第 19b 页 WYG0799-0018d.png WYG0799-0019a.png

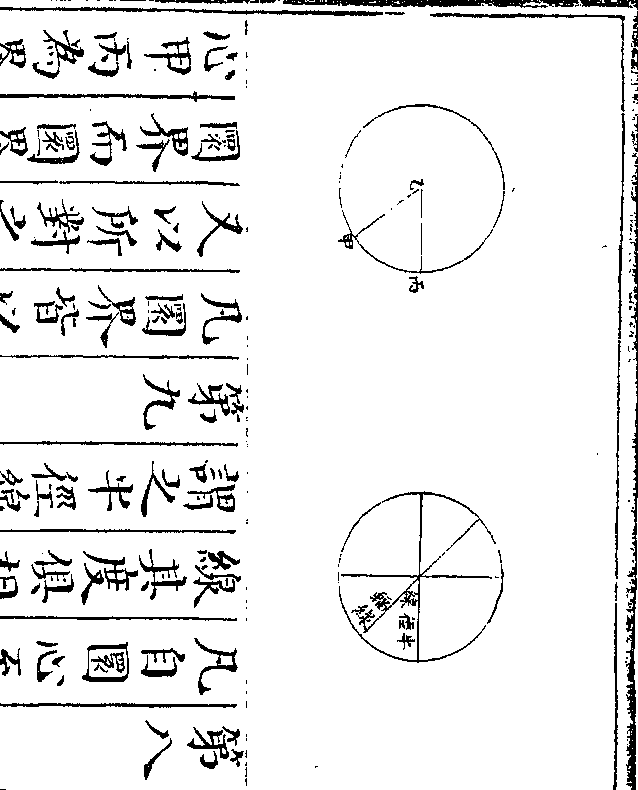
 方数为典以方出圆
方数为典以方出圆典则也言圆之数奇零不尽不可为则故惟方数
可为典则以方出圆者以方之形度圆之分从方
数中生出圆数即前圆出于方之说也如圆径求
积则以径自乘之为正方形而以方率圆率比例
推之即得圆积是皆以方出圆之理也
笠以写天天青黑地黄赤天数之为笠也青黑为表
丹黄为里以象天地之位
此即仪象以表天地之形色也笠形圆故以象天
卷一 第 19b 页 WYG0799-0018d.png WYG0799-0019a.png

 写象也青黑天之色黄赤地之色天数之为笠形
写象也青黑天之色黄赤地之色天数之为笠形卷一 第 20a 页 WYG0799-0019c.png
 则以青黑为表丹黄为里以象天地之位盖取天
则以青黑为表丹黄为里以象天地之位盖取天包地之象也
是故知地者智知天者圣智出于勾勾出于矩夫矩
之于数其裁制万物惟所为耳
天地之高深广远非圣智不能知然圣智非由理
之自然亦不能无所凭藉而知也故明勾股之数
即可以知地而为智知地之数即可因地以知天
而为圣矣故曰智出于勾也然勾股之形又赖矩
卷一 第 20b 页 WYG0799-0019d.png WYG0799-0020a.png

 以成故矩为勾股之本而天地之高深广远皆赖
以成故矩为勾股之本而天地之高深广远皆赖矩以测况万物之大小巨细岂能外于矩之度分
乎故矩之于数其裁制万物惟其所为而无不可
也
周公曰善哉
以周公之圣而与之曰善哉则其得数之本立法
之妙可谓至矣至是而周髀之义尽矣
卷一 第 20b 页 WYG0799-0019d.png WYG0799-0020a.png

 御制数理精蕴上编卷一
御制数理精蕴上编卷一