声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
御制数理精蕴 下编卷八 第 1a 页 WYG0799-0544a.png
 钦定四库全书
钦定四库全书御制数理精蕴下编卷八
线部六
盈朒(单法/) (双套/)
御制数理精蕴 下编卷八 第 2a 页 WYG0799-0545a.png
 盈朒
盈朒盈有馀也朒不足也设有馀不足以求适中亦为因
较而得正数之法此固比例法也但比例以实数求
实数而盈朒则以虚数求实数然虚数皆与实数相
较而生盈朒之差则虚数亦实数也比例以所有之
三率求所馀之一率而盈朒则所有为两数且两数
之中各藏一数其实亦三率也其间有一盈一朒者
则以两数相加为相较之率有两盈或两朒者则以
御制数理精蕴 下编卷八 第 2b 页 WYG0799-0545b.png WYG0799-0545c.png

 两数相减为相较之率有一盈一适足或一朒一适
两数相减为相较之率有一盈一适足或一朒一适足者则无可加减而或盈或朒之数即其较也法不
一致惟在相较以得其差理本一原惟在互比以得
其实错综变幻其用不穷所谓以实御虚和较互见
者庶几尽于此矣
一盈一朒
设如有人分银不知人数亦不知银数只云每人七
两分之则馀四两每人九两分之则少十二两问
人数及银数各若干
御制数理精蕴 下编卷八 第 2b 页 WYG0799-0545b.png WYG0799-0545c.png

 法以七两与九两相减馀二两为一率
法以七两与九两相减馀二两为一率御制数理精蕴 下编卷八 第 3a 页 WYG0799-0546a.png
 一人为二率盈四两与朒十二两相加
一人为二率盈四两与朒十二两相加共十六两为三率推得四率八即为人
数以八人与每人七两相乘得五十六
两加盈四两得六十两即为银数或以
八人与每人九两相乘得七十二两减
朒十二两馀六十两亦为银数也此法
盖因前设分七两后设分九两是每一
人多分二两也然每人分七两则总银
御制数理精蕴 下编卷八 第 3b 页 WYG0799-0546b.png WYG0799-0546c.png

 盈四两每人分九两则总银朒十二两
盈四两每人分九两则总银朒十二两是盈朒相差共十六两矣夫一人多分
二两而总银差十六两则二两为一人
之所多而十六两为八人之所多可知
矣故二两与一人之比同于十六两与
八人之比而为比例四率也既得人数
以每人七两计之则八人应得五十六
两因银尚馀四两故加四两得六十两
为银数也若以每人九两计之则八人
御制数理精蕴 下编卷八 第 3b 页 WYG0799-0546b.png WYG0799-0546c.png

 应得七十二两因银少十二两故减十
应得七十二两因银少十二两故减十御制数理精蕴 下编卷八 第 4a 页 WYG0799-0547a.png
 二两馀六十两为银数也此先得人数
二两馀六十两为银数也此先得人数之法也
又先得银数之法用互乘以齐其分以
九两乘盈四两为加九倍得盈三十六
两以七两乘朒十二两为加七倍得朒
八十四两相加得一百二十两为二率
七倍与九倍相减馀二倍为一率一倍
为三率推得四率六十两即为银数既
御制数理精蕴 下编卷八 第 4b 页 WYG0799-0547b.png WYG0799-0547c.png

 得银数则于六十两内减盈四两馀五
得银数则于六十两内减盈四两馀五十六两以每人七两除之得八为人数
或于六十两加朒十二两共七十二两
以每人九两除之亦得八为人数也此
法以九两互乘盈四两者将盈四两加
九倍也盈四两加九倍则为盈三十六
两既以盈数加九倍则总银数与所分
七两亦皆当加九倍七两加九倍则为
六十三两是则九倍之总银每人六十
御制数理精蕴 下编卷八 第 4b 页 WYG0799-0547b.png WYG0799-0547c.png

 三两分之盈三十六两也以七两互乘
三两分之盈三十六两也以七两互乘御制数理精蕴 下编卷八 第 5a 页 WYG0799-0548a.png
 朒十二两者将朒十二两加七倍也朒
朒十二两者将朒十二两加七倍也朒十二两加七倍则为朒八十四两既以
朒数加七倍则总银数与所分九两亦
皆当加七倍九两加七倍则亦为六十
三两是则七倍之总银每人六十三两
分之朒八十四两也夫每人既皆分六
十三两则是所分之加倍共银数亦必
相同然九倍银数则盈七倍银数则朒
御制数理精蕴 下编卷八 第 5b 页 WYG0799-0548b.png WYG0799-0548c.png

 因九倍比七倍多二倍是盈朒相加之
因九倍比七倍多二倍是盈朒相加之一百二十两即此二倍之银数也知二
倍为一百二十两即知一倍之为几何
矣故以二为一率一百二十两为二率
一为三率推得四率六十两为银数也
既得银数则于六十两内减盈四两馀
五十六两即为分七两者之共数而以
七两除之得八人或于六十两加朒十
二两得七十二两即为分九两者之共
御制数理精蕴 下编卷八 第 5b 页 WYG0799-0548b.png WYG0799-0548c.png

 数而以九两除之亦得八人也此先得
数而以九两除之亦得八人也此先得御制数理精蕴 下编卷八 第 6a 页 WYG0799-0549a.png
 银数之法也
银数之法也又法将盈四两与朒十二两相加得十
六两为一率七两与九两相减馀二两
为二率盈四两为三率得四率五钱与
所分七两相加得七两五钱为每人应
得之数又以五钱除盈四两得八为人
数或仍以十六两为一率二两为二率
以朒十二两为三率得四率一两五钱
御制数理精蕴 下编卷八 第 6b 页 WYG0799-0549b.png WYG0799-0549c.png

 与所分九两相减亦得七两五钱为每
与所分九两相减亦得七两五钱为每人应得之数又以一两五钱除朒十二
两亦得八为人数以八人与每人七两
五钱相乘得六十两为银数也此法盖
因九两与七两相较差二两盈四两与
朒十二两相并为十六两是总银盈朒
共差十六两由于每人之多二两也今
银尚盈四两则每人分七两者其每一
分应多五钱而为七两五钱矣故十六
御制数理精蕴 下编卷八 第 6b 页 WYG0799-0549b.png WYG0799-0549c.png

 两与二两之比同于四两与五钱之比
两与二两之比同于四两与五钱之比御制数理精蕴 下编卷八 第 7a 页 WYG0799-0550a.png
 而为比例四率也且一人多五钱而共
而为比例四率也且一人多五钱而共多四两则其为八人可知矣故五钱与
一人之比同于四两与八人之比亦为
比例四率也若以朒数论之则总银共
差十六两者由于每人少二两今银朒
十二两则每人分九两者其每一分应
少一两五钱而为七两五钱矣且一人
少一两五钱而共少十二两则其为八
御制数理精蕴 下编卷八 第 7b 页 WYG0799-0550b.png WYG0799-0550c.png

 人又可知矣既得人数则以八人与每
人又可知矣既得人数则以八人与每人七两五钱相乘得六十两而为总银
数也此先得每一人所得银数之法也
要之第一法先求人数第二法先求物
价第三法先求适足之数立法虽各不
同而各先得其一一得而无不得者实
由于理之一贯者也
设如众人共出银买物不知人数亦不知物价只云
每人出银四两则不足四两每人出银六两则多
御制数理精蕴 下编卷八 第 7b 页 WYG0799-0550b.png WYG0799-0550c.png

 六两问人数及物价各若干
六两问人数及物价各若干御制数理精蕴 下编卷八 第 8a 页 WYG0799-0551a.png
 法以出四两与出六两相减馀二两为
法以出四两与出六两相减馀二两为一率一人为二率朒四两与盈六两相
加共十两为三率推得四率五即为人
数以五人与每人四两相乘得二十两
加朒四两共得二十四两即为物价或
以五人与每人六两相乘得三十两减
盈六两亦得二十四两为物价也此法
盖因前设出四两后设出六两是每一
御制数理精蕴 下编卷八 第 8b 页 WYG0799-0551b.png WYG0799-0551c.png

 人多出二两也然出四两则朒四两出
人多出二两也然出四两则朒四两出六两则盈六两是盈朒相差共多十两
矣夫一人多出二两而总价即多十两
则二两为一人之所多而十两为几人
之所多可知矣故以比例四率求之而
得五人也既得人数以每人出四两计
之则五人应出二十两因于物价朒四
两故加四两得二十四两为物价若以
每人出六两计之则五人应出三十两
御制数理精蕴 下编卷八 第 8b 页 WYG0799-0551b.png WYG0799-0551c.png

 因于物价盈六两故减六两亦得二十
因于物价盈六两故减六两亦得二十御制数理精蕴 下编卷八 第 9a 页 WYG0799-0552a.png
 四两为物价也此法与首题第一法盈
四两为物价也此法与首题第一法盈朒之加减不同者首题以共人所分共
银为问故分少则总银必盈分多则总
银必朒其所谓盈朒者乃银数之盈朒
故得人数与分银数相乘加盈减朒而
得银数也此以共人所出共银为问故
出少则比物价为朒出多则比物价为
盈其所谓盈朒者乃出数之盈朒故得
御制数理精蕴 下编卷八 第 9b 页 WYG0799-0552b.png WYG0799-0552c.png

 人数与出银数相乘减盈加朒而得物
人数与出银数相乘减盈加朒而得物价也法总一理但加减盈朒之间少不
同耳
又先得银数之法以六两乘朒四两为
加六倍得朒二十四两以四两乘盈六
两为加四倍得盈二十四两相加得四
十八两为二率四倍与六倍相减馀二
倍为一率一倍为三率推得四率二十
四两即为物价既得物价则于二十四
御制数理精蕴 下编卷八 第 9b 页 WYG0799-0552b.png WYG0799-0552c.png

 两内减朒四两馀二十两以每人四两
两内减朒四两馀二十两以每人四两御制数理精蕴 下编卷八 第 10a 页 WYG0799-0553a.png
 除之得五即为人数或于二十四两加
除之得五即为人数或于二十四两加盈六两共三十两以每人六两除之亦
得五为人数也此法盖将朒四两加六
倍为二十四两则物价亦当加六倍而
出四两者亦必加六倍而为出二十四
两矣将盈六两加四倍为二十四两则
物价亦当加四倍而出六两者亦必加
四倍而为出二十四两矣夫每人同出
御制数理精蕴 下编卷八 第 10b 页 WYG0799-0553b.png WYG0799-0553c.png

 二十四两则其加倍共出之数亦必相
二十四两则其加倍共出之数亦必相同然比六倍物价则朒比四倍物价则
盈者因六倍比四倍多二倍是盈朒相
差之四十八两即二倍物价也故以二
为一率四十八两为二率一为三率推
得四率二十四两为物价也既得物价
则于二十四两减朒四两馀二十两即
为出四两者所共出之数而以四两除
之得五人或于二十四两加盈六两共
御制数理精蕴 下编卷八 第 10b 页 WYG0799-0553b.png WYG0799-0553c.png

 三十两即为出六两者所共出之数而
三十两即为出六两者所共出之数而御制数理精蕴 下编卷八 第 11a 页 WYG0799-0554a.png
 以六两除之亦得五人也
以六两除之亦得五人也又法将朒四两与盈六两相加共十两
为一率将出四两与出六两相减馀二
两为二率朒四两为三率得四率八钱
与出四两相加得四两八钱为每人应
出之数又以八钱除朒四两得五为人
数或仍以十两为一率二两为二率盈
六两为三率得四率一两二钱于出六
御制数理精蕴 下编卷八 第 11b 页 WYG0799-0554b.png WYG0799-0554c.png

 两内减之馀四两八钱亦为每人应出
两内减之馀四两八钱亦为每人应出之数又以一两二钱除盈六两亦得五
为人数以五人与四两八钱相乘得二
十四两为物价也此法盖因盈朒之相
差十两由于每人之多二两今欲补足
所朒之四两则每人应多八钱若欲损
所盈之六两则每人应少一两二钱故
十两与二两之比同于四两与八钱之
比亦同于六两与一两二钱之比也且
御制数理精蕴 下编卷八 第 11b 页 WYG0799-0554b.png WYG0799-0554c.png

 一人多八钱即益所朒之四两一人减
一人多八钱即益所朒之四两一人减御制数理精蕴 下编卷八 第 12a 页 WYG0799-0555a.png
 一两二钱即损所盈之六两则其为五
一两二钱即损所盈之六两则其为五人也可知矣既得人数则以五人与每
人四两八钱相乘得二十四两而为物
价之总银也
设如众人乘船渡河每一船载十三人则馀十二人
若每一船载十八人则馀一船问共人数及船数
各若干
法以馀十二人为盈十二人馀一船为
御制数理精蕴 下编卷八 第 12b 页 WYG0799-0555b.png WYG0799-0555c.png

 朒十八人乃以每船所载十三人与每
朒十八人乃以每船所载十三人与每船所载十八人相减馀五人为一率一
船为二率盈十二人与朒十八人相加
共三十人为三率推得四率六即为船
数以六船与每船载十三人相乘得七
十八人加盈十二人得九十为人数或
以六船与每船十八人相乘得一百零
八人减朒十八人亦馀九十为人数也
盖每一船多载五人而盈朒相差为三
御制数理精蕴 下编卷八 第 12b 页 WYG0799-0555b.png WYG0799-0555c.png

 十人故五人与一船之比同于三十人
十人故五人与一船之比同于三十人御制数理精蕴 下编卷八 第 13a 页 WYG0799-0556a.png
 与六船之比也以每船十三人计之六
与六船之比也以每船十三人计之六船共载七十八人加无船之十二人共
九十人以每船十八人计之六船应载
一百零八人因一船无人则减去十八
人馀九十人或减一船馀五船与十八
人相乘亦得九十人也
又先得人数之法以每船载十八人乘
盈十二人为加十八倍得盈二百一十
御制数理精蕴 下编卷八 第 13b 页 WYG0799-0556b.png WYG0799-0556c.png

 六人又以每船载十三人乘朒十八人
六人又以每船载十三人乘朒十八人为加十三倍得朒二百三十四人二数
相加得四百五十人为二率以十三倍
与十八倍相减馀五倍为一率一倍为
三率推得四率九十即为人数减盈十
二人馀七十八人以每船十三人除之
得六为船数或于九十人加朒十八人
共一百零八人以每船十八人除之亦
得六为船数也盖十八人与十三人互
御制数理精蕴 下编卷八 第 13b 页 WYG0799-0556b.png WYG0799-0556c.png

 乘皆得二百三十四人而十二人加十
乘皆得二百三十四人而十二人加十御制数理精蕴 下编卷八 第 14a 页 WYG0799-0557a.png
 八倍则共人数之加十八倍者为每船
八倍则共人数之加十八倍者为每船二百三十四人馀二百一十六人也若
以十八人加十三倍则共人数之加十
三倍者为每船二百三十四人又少二
百三十四人也(二百三十四人为/一船所载之人分)十八
倍比十三倍多五倍是盈朒相差之共
四百五十人即五倍人数故五倍与四
百五十人之比即如一倍与九十人之
御制数理精蕴 下编卷八 第 14b 页 WYG0799-0557b.png WYG0799-0557c.png

 比也既得人数减去所馀之十二人以
比也既得人数减去所馀之十二人以每船十三人除之得船数或加一船之
十八人以每船十八人除之亦得船数
焉
又法将盈十二人与朒十八人相加得
三十人为一率十三人与十八人相减
馀五人为二率盈十二人为三率得四
率二人与每船十三人相加得十五人
为每船应载之数又以二人除盈十二
御制数理精蕴 下编卷八 第 14b 页 WYG0799-0557b.png WYG0799-0557c.png

 人得六为船数或仍以三十人为一率
人得六为船数或仍以三十人为一率御制数理精蕴 下编卷八 第 15a 页 WYG0799-0558a.png
 五人为二率以朒十八人为三率得四
五人为二率以朒十八人为三率得四率三人与每船十八人相减馀十五人
为每船应载之数又以三人除十八人
亦得六为船数以六船与每船十五人
相乘得九十为人数也盖盈朒之相差
三十人由每船多五人今欲合载所盈
之十二人则每船十三人者应加二人
而为十五人欲分载所朒之十八人则
御制数理精蕴 下编卷八 第 15b 页 WYG0799-0558b.png WYG0799-0558c.png
 每船十八人者应减三人而为十五人
每船十八人者应减三人而为十五人也且一船加二人即合载十二人一船
减三人即分载十八人则其为六船也
可知矣
两盈
设如有人分果不知人数亦不知果数只云每人十
二枚盈十二枚每人十三枚盈六枚问人数与果
数各若干
法以每人十二枚与十三枚相减馀一
御制数理精蕴 下编卷八 第 15b 页 WYG0799-0558b.png WYG0799-0558c.png

 枚为一率一人为二率以盈六枚与盈
枚为一率一人为二率以盈六枚与盈御制数理精蕴 下编卷八 第 16a 页 WYG0799-0559a.png
 十二枚相减馀六枚为三率推得四率
十二枚相减馀六枚为三率推得四率六为人数以六人与十二枚相乘得七
十二枚加盈十二枚得八十四枚为果
数若以六人与十三枚相乘得七十八
枚加盈六枚亦得八十四枚为果数也
盖一人多一枚而两盈相差六枚其为
六人可知故凡所分之数相减馀一者
其盈朒之差即人数也
御制数理精蕴 下编卷八 第 16b 页 WYG0799-0559b.png WYG0799-0559c.png
 又先得果数之法以十三枚乘盈十二
又先得果数之法以十三枚乘盈十二枚为加十三倍得盈一百五十六枚以
十二枚乘盈六枚为加十二倍得盈七
十二枚相减馀八十四枚为二率十二
倍与十三倍相减馀一倍为一率仍以
一倍为三率推得四率八十四枚为果
数内减盈十二枚馀七十二枚以每人
十二枚除之得六为人数若于八十四
枚减盈六枚馀七十八枚以每人十三
御制数理精蕴 下编卷八 第 16b 页 WYG0799-0559b.png WYG0799-0559c.png

 枚除之亦得六为人数也盖十二倍比
枚除之亦得六为人数也盖十二倍比御制数理精蕴 下编卷八 第 17a 页 WYG0799-0560a.png
 十三倍差一倍则盈朒相差八十四枚
十三倍差一倍则盈朒相差八十四枚即一倍之果数故凡互乘差一倍者则
互乘所得盈朒之差即为总数既得人
数又得总数则以人数除总数即得每
人所分之数矣
又法以两盈数相减为一率互乘所得
之两盈数相减为二率一人为三率得
四率即为每人所应得之数也此题前
御制数理精蕴 下编卷八 第 17b 页 WYG0799-0560b.png WYG0799-0560c.png

 二法固以两盈相减即为人数互乘所
二法固以两盈相减即为人数互乘所得两盈相减即为总数盖因十二与十
三相减馀一数故也其或馀几数者亦
即为几倍人数或为几倍总数其以人
数除总数即同于以几倍人数除几倍
总数也
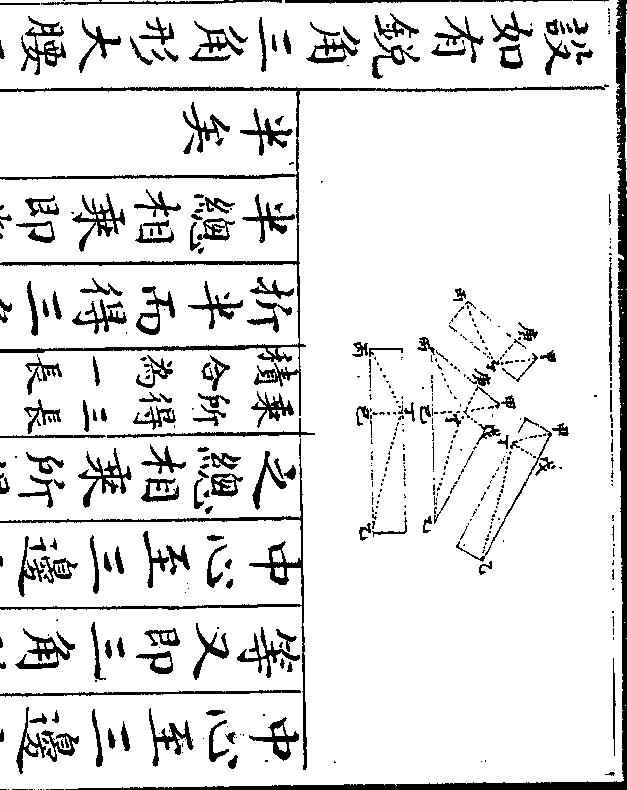
设如有缎一疋欲作新帐幔一架先摺作六幅每幅
比旧制长一尺二寸后摺作七幅每幅比旧制长
二寸问缎之长及旧帐之长各若干
御制数理精蕴 下编卷八 第 17b 页 WYG0799-0560b.png WYG0799-0560c.png

 法以长一尺二寸用六幅因之得盈七
法以长一尺二寸用六幅因之得盈七御制数理精蕴 下编卷八 第 18a 页 WYG0799-0561a.png
 尺二寸以长二寸用七幅因之得盈一
尺二寸以长二寸用七幅因之得盈一尺四寸乃以六幅与七幅相减馀一幅
为一率一尺四寸与七尺二寸相减馀
五尺八寸为二率一幅为三率推得四
率五尺八寸为旧帐之长加盈一尺二
寸共七尺以六幅乘之得四十二尺为
缎之长也(若于五尺八寸加二寸得六/尺以七幅乘之亦得四十二)
(尺/)盖摺作六幅每幅盈一尺二寸是六
御制数理精蕴 下编卷八 第 18b 页 WYG0799-0561b.png WYG0799-0561c.png

 幅共盈七尺二寸也摺作七幅每幅盈
幅共盈七尺二寸也摺作七幅每幅盈二寸是七幅共盈一尺四寸也七幅比
六幅多一幅而两盈相差五尺八寸且
两盈之数皆比旧帐为盈则五尺八寸
为旧帐之长可知矣既得旧帐之数则
加一尺二寸而以六幅乘之即得缎之
长数也或以六幅与五尺八寸相乘加
盈七尺二寸亦得缎之长数盖七尺二
寸者原系六因一尺二寸所得之数则
御制数理精蕴 下编卷八 第 18b 页 WYG0799-0561b.png WYG0799-0561c.png

 加于旧帐而总乘之与各乘其数而后
加于旧帐而总乘之与各乘其数而后御制数理精蕴 下编卷八 第 19a 页 WYG0799-0562a.png
 加之一也若以七幅算之其理亦同
加之一也若以七幅算之其理亦同又先得缎之长法以七幅乘盈七尺二
寸为加七倍得盈五十尺零四寸以六
幅乘盈一尺四寸为加六倍得盈八尺
四寸相减馀四十二尺为二率六倍与
七倍相减馀一倍为一率仍以一倍为
三率推得四率四十二尺为缎之长减
盈七尺二寸以六幅除之得五尺八寸
御制数理精蕴 下编卷八 第 19b 页 WYG0799-0562b.png WYG0799-0562c.png

 为旧帐之长也(若减盈一尺四寸以七/幅除之亦得五尺八寸)
为旧帐之长也(若减盈一尺四寸以七/幅除之亦得五尺八寸)盖将六幅加七倍七幅加六倍皆得四
十二幅是七倍缎之长比旧帐四十二
幅长五十尺零四寸六倍缎之长比旧
帐四十二幅长八尺四寸是两盈相差
四十二尺即一倍缎之长也既得缎之
长则减其共盈数而以幅数除之即得
旧帐之长或先以幅数除之而减其每
幅之盈亦得旧帐之长也
御制数理精蕴 下编卷八 第 19b 页 WYG0799-0562b.png WYG0799-0562c.png

 两朒
两朒御制数理精蕴 下编卷八 第 20a 页 WYG0799-0563a.png
 设如有银买马不知银数亦不知马数但云每一匹
设如有银买马不知银数亦不知马数但云每一匹十五两不足八十两每一匹十三两仍不足十六
两问马数及银数各若干
法以十三两与十五两相减馀二两为
一率一马为二率朒十六两与朒八十
两相减馀六十四两为三率推得四率
三十二为马数以三十二匹与每匹十
五两相乘得四百八十两减朒八十两
御制数理精蕴 下编卷八 第 20b 页 WYG0799-0563b.png WYG0799-0563c.png
 得四百两为银数若以三十二匹与每
得四百两为银数若以三十二匹与每匹十三两相乘得四百一十六两减朒
十六两亦得四百两为银数也盖一马
差二两则总银差六十四两二两与一
马之比即同于六十四两与三十二马
之比也既得马数则与每匹之价相乘
而减其所朒之数即得银数矣
又先得银数之法以十三两乘朒八十
两为加十三倍得朒一千零四十两以
御制数理精蕴 下编卷八 第 20b 页 WYG0799-0563b.png WYG0799-0563c.png

 十五两乘朒十六两为加十五倍得朒
十五两乘朒十六两为加十五倍得朒御制数理精蕴 下编卷八 第 21a 页 WYG0799-0564a.png
 二百四十两相减馀八百两为二率十
二百四十两相减馀八百两为二率十三倍与十五倍相减馀二倍为一率一
倍为三率推得四率四百两为银数加
朒八十两共四百八十两以每匹十五
两除之得三十二为马数或于四百两
加朒十六两共四百一十六两以每匹
十三两除之亦得三十二为马数也盖
将十五两加十三倍十三两加十五倍
御制数理精蕴 下编卷八 第 21b 页 WYG0799-0564b.png WYG0799-0564c.png

 皆得一百九十五两马价齐同祗十三
皆得一百九十五两马价齐同祗十三倍银数则朒一千零四十两十五倍银
数则朒二百四十两是两朒相差八百
两即二倍之银数故以四率求之而得
银数也既得银数则加其所朒之数以
每匹之价除之即得马数矣
设如有米易布不知米数亦不知布数但云易布二
十疋则米少一石易布十六疋则米仍少二斗问
米数及布数各若干
御制数理精蕴 下编卷八 第 21b 页 WYG0799-0564b.png WYG0799-0564c.png

 法以十六疋与二十疋相减馀四疋为
法以十六疋与二十疋相减馀四疋为御制数理精蕴 下编卷八 第 22a 页 WYG0799-0565a.png
 一率二斗与一石相减馀八斗为二率
一率二斗与一石相减馀八斗为二率一疋为三率推得四率二斗为布每疋
所值米数以二斗与二十疋相乘得四
石减朒一石馀三石为米数若以二斗
与十六疋相乘得三石二斗减朒二斗
亦馀三石为米数既得米数以每疋二
斗除之得十五疋为布数也
又先得米数之法以十六疋乘朒一石
御制数理精蕴 下编卷八 第 22b 页 WYG0799-0565b.png WYG0799-0565c.png

 为加十六倍得朒十六石以二十疋乘
为加十六倍得朒十六石以二十疋乘朒二斗为加二十倍得朒四石相减馀
十二石为二率十六倍与二十倍相减
馀四倍为一率一倍为三率推得四率
三石为米数加朒一石共四石为一率
二十疋为二率三石为三率得四率十
五疋为布数或于三石加朒二斗共三
石二斗为一率十六疋为二率三石为
三率亦得四率十五疋为布数也盖二
御制数理精蕴 下编卷八 第 22b 页 WYG0799-0565b.png WYG0799-0565c.png

 十疋加十六倍十六疋加二十倍皆为
十疋加十六倍十六疋加二十倍皆为御制数理精蕴 下编卷八 第 23a 页 WYG0799-0566a.png
 易布三百二十疋而十六倍其米数则
易布三百二十疋而十六倍其米数则朒十六石二十倍其米数则朒四石是
两朒相差十二石即相差四倍之米数
故以比例求之得米数也既得米数则
加朒一石为四石即足易布二十疋故
四石与二十疋之比同于三石与十五
疋之比也或加朒二斗得三石二斗即
足易布十六疋故三石二斗与十六疋
御制数理精蕴 下编卷八 第 23b 页 WYG0799-0566b.png WYG0799-0566c.png

 之比亦同于三石与十五疋之比也
之比亦同于三石与十五疋之比也又先得布数之法以朒二斗与朒一石
相减馀八斗为一率十六疋与十二疋
相减馀四疋为二率朒一石为三率得
四率五疋与二十疋相减馀十五疋为
布数又以五疋为一率朒一石为二率
十五疋为三率推得四率三石为米数
也若仍以八斗为一率四疋为二率朒
二斗为三率则得四率一疋与十六疋
御制数理精蕴 下编卷八 第 23b 页 WYG0799-0566b.png WYG0799-0566c.png

 相减亦得十五疋为布数又以一疋为
相减亦得十五疋为布数又以一疋为御制数理精蕴 下编卷八 第 24a 页 WYG0799-0567a.png
 一率二斗为二率十五疋为三率亦得
一率二斗为二率十五疋为三率亦得四率三石为米数也此法即先求适足
之理盖十五疋即适足之数也
一盈一适足
设如按户纳粮不知户数亦不知粮数只云每户三
升盈六石每户二升五合适足问人户及粮数各
若干
法以二升五合与三升相减馀五合为
御制数理精蕴 下编卷八 第 24b 页 WYG0799-0567b.png WYG0799-0567c.png

 一率盈六石变为六千合为二率一户
一率盈六石变为六千合为二率一户为三率推得四率一千二百为户数与
每户二升五合相乘得三十石为粮数
也盖每户多五合而总粮多六石其为
一千二百户可知故五合与六石之比
同于一与一千二百之比也(此以一户/为三率者)
(二三率原可互易变/之以明比例之理也)既得户数则与二
升五合相乘适足三十石之数矣若以
一千二百户与每户三升相乘得三十
御制数理精蕴 下编卷八 第 24b 页 WYG0799-0567b.png WYG0799-0567c.png

 六石减盈六石亦得三十石为粮数也
六石减盈六石亦得三十石为粮数也御制数理精蕴 下编卷八 第 25a 页 WYG0799-0568a.png
 又先得粮数之法以二升五合乘盈六
又先得粮数之法以二升五合乘盈六石为加二十五倍(以合为/单位)得盈一百五
十石以三升乘适足为加三十倍仍得
适足(盖全粮一分每户二升五合而适/足若将全粮加三十倍为三十分)
(则二升五合亦当加三十倍为七斗五/升是全粮三十分每户七斗五升仍适)
(足/也)故即以一百五十石为二率将二十
五倍与三十倍相减馀五倍为一率一
倍为三率推得四率三十石为粮数以
御制数理精蕴 下编卷八 第 25b 页 WYG0799-0568b.png WYG0799-0568c.png

 每户二升五合除之得一千二百为户
每户二升五合除之得一千二百为户数或加盈六石为三十六石以每户三
升除之亦得一千二百为户数也
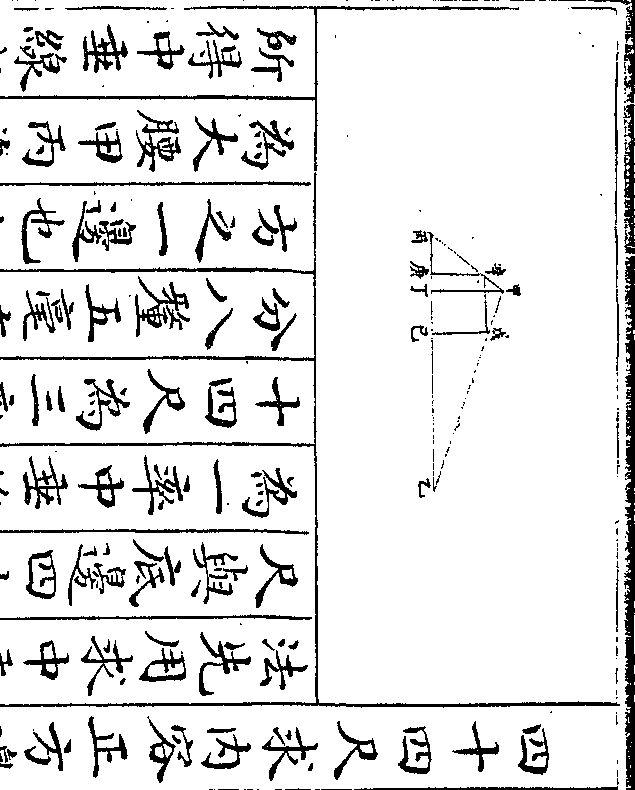
设如有井不知其深有绳不知其长只云将绳作三
摺入井长八尺将绳作五摺入井适足问井深绳
长各若干
法以三摺与五摺相减馀二摺为一率
长八尺用三摺因之得盈二丈四尺为
二率一摺为三率推得四率一丈二尺
御制数理精蕴 下编卷八 第 25b 页 WYG0799-0568b.png WYG0799-0568c.png

 为井深以五摺乘之得六丈为绳长或
为井深以五摺乘之得六丈为绳长或御制数理精蕴 下编卷八 第 26a 页 WYG0799-0569a.png
 以三摺乘之加盈二丈四尺亦得六丈
以三摺乘之加盈二丈四尺亦得六丈为绳长也盖摺作三摺每摺盈八尺是
三摺共盈二丈四尺也五摺比三摺多
二摺而盈与适足无可加减则盈二丈
四尺即为二摺之数其一摺为一丈二
尺矣井深既为五摺之一故一摺之数
即为井深之数也既得井深则以五摺
乘之得绳长之数或以三摺乘之加盈
御制数理精蕴 下编卷八 第 26b 页 WYG0799-0569b.png WYG0799-0569c.png

 二丈四尺亦得绳长之数也
二丈四尺亦得绳长之数也又先得绳长之法以五摺乘盈二丈四
尺为加五倍得盈一十二丈以三摺乘
适足为加三倍仍得适足故即以一十
二丈为二率三倍与五倍相减馀二倍
为一率一倍为三率推得四率六丈为
绳长以五摺除之得一丈二尺为井深
或减盈二丈四尺馀三丈六尺以三摺
除之亦得一丈二尺为井深也
御制数理精蕴 下编卷八 第 26b 页 WYG0799-0569b.png WYG0799-0569c.png

 一朒一适足
一朒一适足御制数理精蕴 下编卷八 第 27a 页 WYG0799-0570a.png
 设如计日登程不知日数亦不知路程只云每日行
设如计日登程不知日数亦不知路程只云每日行五十五里则离所欲至之地共差六十里每日行
六十里适足问日数及路程各若干
法以五十五里与六十里相减馀五里
为一率一日为二率朒六十里为三率
推得四率十二为日数与每日六十里
相乘得七百二十里为路数若以日数
十二与每日行五十五里相乘得六百
御制数理精蕴 下编卷八 第 27b 页 WYG0799-0570b.png WYG0799-0570c.png

 六十里是不到六十里也加朒六十里
六十里是不到六十里也加朒六十里亦得七百二十里也
又先得路程之法以六十里乘朒六十
里为加六十倍得朒三千六百里以五
十五里乘适足为加五十五倍仍得适
足故即以三千六百里为二率五十五
倍与六十倍相减馀五倍为一率一倍
为三率推得四率七百二十里为路程
以每日六十里除之得十二为日数或
御制数理精蕴 下编卷八 第 27b 页 WYG0799-0570b.png WYG0799-0570c.png

 于七百二十里内减朒六十里馀六百
于七百二十里内减朒六十里馀六百御制数理精蕴 下编卷八 第 28a 页 WYG0799-0571a.png
 六十里以每日五十五里除之亦得十
六十里以每日五十五里除之亦得十二为日数也
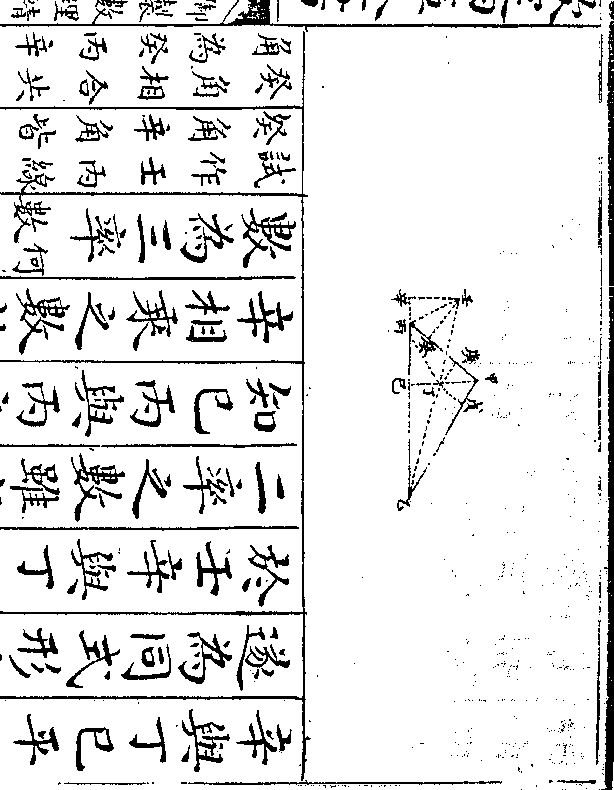
设如有直田一段欲截一头作园只云截长十步不
足三十二步截长十二步适足问截积及原阔各
若干
法以十步与十二步相减馀二步为一
率朒三十二步为二率一步为三率推
得四率十六步为原阔与十二步相乘
御制数理精蕴 下编卷八 第 28b 页 WYG0799-0571b.png WYG0799-0571c.png

 得一百九十二步为截积或与十步相
得一百九十二步为截积或与十步相乘加朒三十二步亦得一百九十二步
为截积也盖长十步则少三十二步长
十二步则适足是三十二步者即长二
步与原阔相乘之积故以二步除之得
原阔也既得原阔则与截长十二步相
乘得截积或与截长十步相乘加朒三
十二步亦得截积也
又先得截积之法以十二步乘朒三十
御制数理精蕴 下编卷八 第 28b 页 WYG0799-0571b.png WYG0799-0571c.png

 二步为加十二倍得朒三百八十四步
二步为加十二倍得朒三百八十四步御制数理精蕴 下编卷八 第 29a 页 WYG0799-0572a.png
 以十步乘适足为加十倍仍得适足故
以十步乘适足为加十倍仍得适足故即以三百八十四步为二率以十倍与
十二倍相减馀二倍为一率一倍为三
率推得四率一百九十二步为截积以
截长十二步除之得十六步为原阔或
于一百九十二步内减朒三十二步馀
一百六十步以截长十步除之亦得十
六步为原阔也
御制数理精蕴 下编卷八 第 30a 页 WYG0799-0572c.png
 双套盈朒
双套盈朒盈朒之法皆以每人几何而盈几何每人几何而朒
几何为问其首数皆为一故以一人之较与共较为
比例而得人数即欲先求共数不过用一互乘以齐
其分而已故为单法若双套则以几人几何而盈几
何几人几何而朒几何为问其首数已不同故必先
用一互乘以齐之而后可以为比若欲先求共数则
用两互乘是以谓之双套至于比例相求之理则仍
御制数理精蕴 下编卷八 第 30b 页 WYG0799-0572d.png WYG0799-0573a.png

 与单法同也
与单法同也一盈一朒
设如有人分银不知人数亦不知银数只云每四人
分银三两则盈六两每六人分银九两则朒三两
问人数与银数各若干
法以四人互乘九两得三十六两以六
人互乘三两得十八两相减馀十八两
为一率四人六人互乘得二十四人为
二率盈六两与朒三两相加得九两为
御制数理精蕴 下编卷八 第 30b 页 WYG0799-0572d.png WYG0799-0573a.png

 三率推得四率十二即为人数既得人
三率推得四率十二即为人数既得人御制数理精蕴 下编卷八 第 31a 页 WYG0799-0573c.png
 数乃以四人为一率三两为二率十二
数乃以四人为一率三两为二率十二人为三率推得四率九两加盈六两得
十五两即为银数或以六人为一率九
两为二率十二人为三率推得四率十
八两减朒三两亦馀十五两为银数也
此法必用互乘以齐其数者盖单法以
所分数相减为一率一人为二率盈朒
相加为三率今三两为四人之所分九
御制数理精蕴 下编卷八 第 31b 页 WYG0799-0573d.png WYG0799-0574a.png

 两为六人之所分不可以相减而为一
两为六人之所分不可以相减而为一率也四人与六人人数不同不可以为
二率也所以必用互乘以齐之一则为
二十四人分十八两虽为加六倍其比
例仍同于四人分三两也一则为二十
四人分三十六两虽为加四倍其比例
仍同于六人分九两也是以十八两与
三十六两相减馀十八两为二十四人
之所差而盈朒差九两即知为几人之
御制数理精蕴 下编卷八 第 31b 页 WYG0799-0573d.png WYG0799-0574a.png

 所差故十八两与二十四人之比即同
所差故十八两与二十四人之比即同御制数理精蕴 下编卷八 第 32a 页 WYG0799-0574c.png
 于九两与十二人之比也既得人数之
于九两与十二人之比也既得人数之后而仍用比例四率者何也盖单法所
分之银数为一人之所分故以人数与
所分之银数相乘加盈减朒而即得总
银今则所分之银数为四人或六人之
所分故每几人与所分几何之比即如
总人与总银之比而得四率加盈减朒
始得总银数也
御制数理精蕴 下编卷八 第 32b 页 WYG0799-0574d.png WYG0799-0575a.png

 又捷法以四人归除三两每一人应得
又捷法以四人归除三两每一人应得七钱五分以六人归除九两每一人应
得一两五钱乃照盈朒单法列之为每
人七钱五分分之盈六两每人一两五
钱分之朒三两是以七钱五分与一两
五钱相减馀七钱五分为一率一人为
二率盈六两与朒三两相加得九两为
三率推得四率十二为人数既得人数
则以一人为一率一两五钱为二率十
御制数理精蕴 下编卷八 第 32b 页 WYG0799-0574d.png WYG0799-0575a.png

 二人为三率推得四率十八两减朒三
二人为三率推得四率十八两减朒三御制数理精蕴 下编卷八 第 33a 页 WYG0799-0575c.png
 两馀十五两为银数也或以每人七钱
两馀十五两为银数也或以每人七钱五分为二率推得四率九两加盈六两
亦得十五两为银数也此法以四人除
三两以六人除九两皆为度尽之数若
数有奇零度不尽者则必用互乘之法
而后可
又先得银数之法以四人互乘九两得
三十六两又以三十六两互乘盈六两
御制数理精蕴 下编卷八 第 33b 页 WYG0799-0575d.png WYG0799-0576a.png

 为加三十六倍得盈二百一十六两以
为加三十六倍得盈二百一十六两以六人互乘三两得一十八两又以一十
八两互乘朒三两为加十八倍得朒五
十四两两数相加得二百七十两为二
率十八倍与三十六倍相减馀十八倍
为一率一倍为三率推得四率十五两
为银数既得银数乃以三两为一率四
人为二率十五两减盈六两馀九两为
三率推得四率十二为人数或以九两
御制数理精蕴 下编卷八 第 33b 页 WYG0799-0575d.png WYG0799-0576a.png

 为一率六人为二率十五两加朒三两
为一率六人为二率十五两加朒三两御制数理精蕴 下编卷八 第 34a 页 WYG0799-0576c.png
 共十八两为三率亦得四率十二为人
共十八两为三率亦得四率十二为人数也盖单法以所分之数相减为一率
以所分之数互乘盈朒之数相减为二
率一倍为三率得四率为银数今则三
两为四人之所分九两为六人之所分
其数不同即三两与九两互乘亦皆得
二十七两而一则为三十六人分二十
七两(加九/倍也)一则为十八人分二十七两
御制数理精蕴 下编卷八 第 34b 页 WYG0799-0576d.png WYG0799-0577a.png

 (加三/倍也)其数亦仍不同不可相为比例故
(加三/倍也)其数亦仍不同不可相为比例故必以四人六人互乘为二十四人以齐
其人数又必以十八与三十六互乘盈
朒之数以齐其所分银数然后人数与
所分银数俱同可以设为比例是以十
八两加三十六倍三十六两加十八倍
皆为六百四十八两即如三十六倍其
银数则每二十四人分六百四十八两
盈二百一十六两若十八倍其银数则
御制数理精蕴 下编卷八 第 34b 页 WYG0799-0576d.png WYG0799-0577a.png

 每二十四人分六百四十八两朒五十
每二十四人分六百四十八两朒五十御制数理精蕴 下编卷八 第 35a 页 WYG0799-0577c.png
 四两也然则盈朒相差二百七十两即
四两也然则盈朒相差二百七十两即十八倍银数之所差矣故十八倍与二
百七十两之比即同于一倍与十五两
之比而为比例四率也既得银数而减
盈加朒为比例四率者盖以所分之银
数与几何人之比即如减盈加朒之总
银数与总人数之比也
又先得银数之法以四人互乘九两得
御制数理精蕴 下编卷八 第 35b 页 WYG0799-0577d.png WYG0799-0578a.png

 三十六两以六人互乘三两得十八两
三十六两以六人互乘三两得十八两相减馀十八两为一率以互乘所得之
十八两为二率盈六两与朒三两相加
得九两为三率推得四率九两加盈六
两得十五两为银数(若以三十六两为/二率则得四率十)
(八两减朒三两亦/得十五两为银数)既得银数则以三两
为一率四人为二率十五两内减盈六
两馀九两为三率推得四率十二为人
数也(若以九两为一率六人为二率十/五两内加朒三两共十八两为三)
御制数理精蕴 下编卷八 第 35b 页 WYG0799-0577d.png WYG0799-0578a.png

 (率亦得四率/十二为人数)此法盖合两四率而为一
(率亦得四率/十二为人数)此法盖合两四率而为一御制数理精蕴 下编卷八 第 36a 页 WYG0799-0578c.png
 四率原法以十八两为一率二十四人
四率原法以十八两为一率二十四人为二率九两为三率得四率十二为人
数又如以二十四人为一率十八两为
二率(与四人为一率三两为二率者/同因其俱为四与三之比例)十
二人为三率则得四率九两加盈六两
得十五两为银数今将两四率合为一
四率则前四率中省以二十四乘后四
率中省以二十四除故以十八两为一
御制数理精蕴 下编卷八 第 36b 页 WYG0799-0578d.png WYG0799-0579a.png

 率又为二率以九两为三率而得四率
率又为二率以九两为三率而得四率九两加盈六两为银数也
设如众人共出银买物不知人数亦不知物价只云
每八人出银七两则盈四两五钱每九人出银六
两则朒三两问人数及物价各若干
法以八人互乘六两得四十八两以九
人互乘七两得六十三两相减馀十五
两为一率八人九人互乘得七十二人
为二率盈四两五钱与朒三两相加得
御制数理精蕴 下编卷八 第 36b 页 WYG0799-0578d.png WYG0799-0579a.png

 七两五钱为三率推得四率三十六即
七两五钱为三率推得四率三十六即御制数理精蕴 下编卷八 第 37a 页 WYG0799-0579c.png
 为人数既得人数乃以八人为一率七
为人数既得人数乃以八人为一率七两为二率三十六人为三率推得四率
三十一两五钱减盈四两五钱馀二十
七两即为物价或以九人为一率六两
为二率三十六人为三率推得四率二
十四两加朒三两亦得二十七两为物
价也此法用互乘以齐其数一则变为
七十二人出六十三两一则变为七十
御制数理精蕴 下编卷八 第 37b 页 WYG0799-0579d.png WYG0799-0580a.png

 二人出四十八两其相差十五两是十
二人出四十八两其相差十五两是十五两为七十二人之所差则盈朒相加
之七两五钱即知为三十六人之所差
故十五两与七十二人之比即同于七
两五钱与三十六人之比也既得人数
仍用比例四率以每几人与所出几何
之比即如总人与总银之比而得数内
减盈加朒即为物价也
又先得银数之法以八人互乘六两得
御制数理精蕴 下编卷八 第 37b 页 WYG0799-0579d.png WYG0799-0580a.png

 四十八两又以四十八两互乘盈四两
四十八两又以四十八两互乘盈四两御制数理精蕴 下编卷八 第 38a 页 WYG0799-0580c.png
 五钱为加四十八倍得盈二百一十六
五钱为加四十八倍得盈二百一十六两以九人互乘七两得六十三两又以
六十三两互乘朒三两为加六十三倍
得朒一百八十九两二数相加得四百
零五两为二率四十八倍与六十三倍
相减馀十五倍为一率一倍为三率推
得四率二十七两为银数既得银数乃
以七两为一率八人为二率二十七两
御制数理精蕴 下编卷八 第 38b 页 WYG0799-0580d.png WYG0799-0581a.png

 内加盈四两五钱共三十一两五钱为
内加盈四两五钱共三十一两五钱为三率推得四率三十六为人数或以六
两为一率九人为二率于二十七两减
朒三两馀二十四两为三率亦得四率
三十六为人数也此法用互乘以齐人
数银数而成比例故八人与九人互乘
皆为七十二人以六十三两与四十八
两互乘皆为出三千零二十四两此数
比四十八倍之物价则盈二百一十六
御制数理精蕴 下编卷八 第 38b 页 WYG0799-0580d.png WYG0799-0581a.png

 两比六十三倍之物价则朒一百八十
两比六十三倍之物价则朒一百八十御制数理精蕴 下编卷八 第 39a 页 WYG0799-0581c.png
 九两其盈朒之相差为四百零五两其
九两其盈朒之相差为四百零五两其四十八倍与六十三倍相差为十五倍
以十五倍与四百零五两之比即同于
一倍与二十七两之比也既得银数仍
用比例四率盖以所出之银数与几何
人之比即如加盈减朒之总银数与总
人数之比也
两盈
御制数理精蕴 下编卷八 第 39b 页 WYG0799-0581d.png WYG0799-0582a.png

 设如众人轮班值日不知人数亦不知日数只云每
设如众人轮班值日不知人数亦不知日数只云每四人值五日则盈二十日每八人值九日仍盈八
日问人数及日数各若干
法以四人互乘九日得三十六日以八
人互乘五日得四十日相减馀四日为
一率四人八人互乘得三十二人为二
率盈八日与盈二十日相减馀十二日
为三率推得四率九十六为人数既得
人数乃以四人为一率五日为二率九
御制数理精蕴 下编卷八 第 39b 页 WYG0799-0581d.png WYG0799-0582a.png

 十六人为三率推得四率一百二十日
十六人为三率推得四率一百二十日御制数理精蕴 下编卷八 第 40a 页 WYG0799-0582c.png
 减盈二十日馀一百为日数或以八人
减盈二十日馀一百为日数或以八人为一率九日为二率九十六人为三率
推得四率一百零八日减盈八日亦馀
一百为日数也此法用互乘以齐其分
一则变为三十二人值四十日一则变
为三十二人值三十六日其相差为四
日知四日为三十二人之所差则两盈
相减之十二日即知为九十六人之所
御制数理精蕴 下编卷八 第 40b 页 WYG0799-0582d.png WYG0799-0583a.png

 差矣既得人数则以每几人与值几日
差矣既得人数则以每几人与值几日之比即同于总人与总日之比而于得
数之内减其所盈即为日数也
又先得日数之法以四人互乘九日得
三十六日又以三十六日互乘盈二十
日为加三十六倍得盈七百二十日以
八人互乘五日得四十日又以四十日
互乘盈八日为加四十倍得盈三百二
十日相减馀四百日为二率三十六倍
御制数理精蕴 下编卷八 第 40b 页 WYG0799-0582d.png WYG0799-0583a.png

 与四十倍相减馀四倍为一率一倍为
与四十倍相减馀四倍为一率一倍为御制数理精蕴 下编卷八 第 41a 页 WYG0799-0583c.png
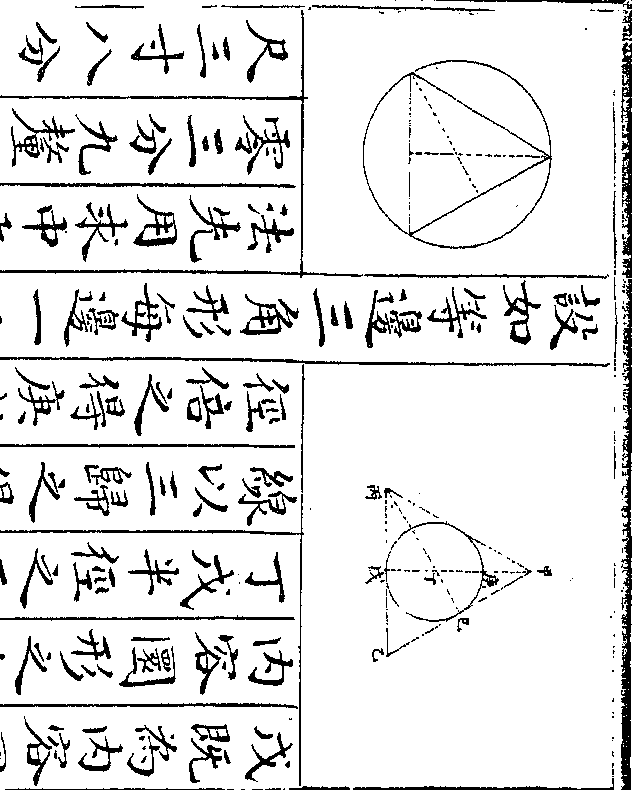
 三率推得四率一百为日数既得日数
三率推得四率一百为日数既得日数乃以五日为一率四人为二率一百日
内加盈二十日共一百二十日为三率
推得四率九十六为人数或以九日为
一率八人为二率一百日内加盈八日
共一百零八日为三率亦得四率九十
六为人数也盖八人四人互乘皆为三
十二人三十六日四十日互乘皆为一
御制数理精蕴 下编卷八 第 41b 页 WYG0799-0583d.png WYG0799-0584a.png

 千四百四十日然比三十六倍日数则
千四百四十日然比三十六倍日数则盈七百二十日比四十倍日数则盈三
百二十日二数相差为四百日三十六
倍与四十倍相差为四倍知四倍之为
四百日即知一倍之为一百日矣既得
日数则以所值之几日与几人之比即
同于加盈之总日数与总人数之比也
两朒
设如有人分绢分之不尽只云每三人五疋少二十
御制数理精蕴 下编卷八 第 41b 页 WYG0799-0583d.png WYG0799-0584a.png

 疋每六人九疋少十疋问人数及绢数各若干
疋每六人九疋少十疋问人数及绢数各若干御制数理精蕴 下编卷八 第 42a 页 WYG0799-0584c.png
 法以三人互乘九疋得二十七疋以六
法以三人互乘九疋得二十七疋以六人互乘五疋得三十疋相减馀三疋为
一率三人六人互乘得一十八人为二
率朒十疋与朒二十疋相减馀十疋为
三率推得四率六十为人数既得人数
则以三人为一率五疋为二率六十人
为三率推得四率一百疋减朒二十疋
馀八十疋为绢数若以六人为一率九
御制数理精蕴 下编卷八 第 42b 页 WYG0799-0584d.png WYG0799-0585a.png

 疋为二率六十人为三率推得四率九
疋为二率六十人为三率推得四率九十疋减朒十疋亦得八十疋为绢数也
此法用互乘以齐其数一则变为十八
人分三十疋朒二十疋一则变为十八
人分二十七疋朒十疋三十疋比二十
七疋相差三疋朒二十疋比朒十疋相
差十疋知三疋为十八人之所差即知
十疋为六十人之所差故三疋与十八
人之比即同于十疋与六十人之比也
御制数理精蕴 下编卷八 第 42b 页 WYG0799-0584d.png WYG0799-0585a.png

 又先得绢数之法以三人乘九疋得二
又先得绢数之法以三人乘九疋得二御制数理精蕴 下编卷八 第 43a 页 WYG0799-0585c.png
 十七疋六人乘五疋得三十疋相减馀
十七疋六人乘五疋得三十疋相减馀三疋为一率三十疋为二率朒十疋与
朒二十疋相减馀十疋为三率推得四
率一百疋减朒二十疋馀八十疋为绢
数也(若以二十七疋为二率则求得四/率九十疋减
(为绢/数)既得绢数则加朒二十疋共一百
疋为三率五疋为一率三人为二率推
得四率六十为人数也此法亦合两四
御制数理精蕴 下编卷八 第 43b 页 WYG0799-0585d.png WYG0799-0586a.png

 率而为一四率盖原法以三疋为一率
率而为一四率盖原法以三疋为一率十八人为二率十疋为三率得四率六
十为人数又如以十八人为一率三十
疋为二率(与三人为一率五疋为二率/者同因其俱为三与五之比)
(例/)六十人为三率得四率一百疋减朒
二十疋馀八十疋为绢数今合两四率
为一四率则前四率中省以一十八乘
后四率中省以一十八除也
一盈一适足
御制数理精蕴 下编卷八 第 43b 页 WYG0799-0585d.png WYG0799-0586a.png

 设如众人支粮每三人支九石盈五十四石每四人
设如众人支粮每三人支九石盈五十四石每四人御制数理精蕴 下编卷八 第 44a 页 WYG0799-0586c.png
 支十四石适足问人数与粮数各若干
支十四石适足问人数与粮数各若干法以三人互乘十四石得四十二石以
四人互乘九石得三十六石相减馀六
石为一率三人四人互乘得十二人为
二率盈与适足无可加减即以盈五十
四石为三率推得四率一百零八为人
数既得人数乃以四人为一率十四石
为二率一百零八人为三率推得四率
御制数理精蕴 下编卷八 第 44b 页 WYG0799-0586d.png WYG0799-0587a.png

 三百七十八石为粮数或以三人为一
三百七十八石为粮数或以三人为一率九石为二率一百零八人为三率推
得四率三百二十四石加盈五十四石
亦得三百七十八石为粮数也此法用
互乘以齐其分一则变为十二人支三
十六石一则变为十二人支四十二石
其相差六石知六石为十二人之所差
即知五十四石为一百零八人之所差
矣既得人数则以每几人与支几石之
御制数理精蕴 下编卷八 第 44b 页 WYG0799-0586d.png WYG0799-0587a.png

 比即同于总人数与总粮数之比也
比即同于总人数与总粮数之比也御制数理精蕴 下编卷八 第 45a 页 WYG0799-0587c.png
 又先得粮数之法以三人互乘十四石
又先得粮数之法以三人互乘十四石得四十二石又以四十二石互乘盈五
十四石为加四十二倍得盈二千二百
六十八石以四人互乘九石得三十六
石又以三十六石互乘适足为加三十
六倍仍得适足故即以盈二千二百六
十八石为二率三十六倍与四十二倍
相减馀六倍为一率一倍为三率推得
御制数理精蕴 下编卷八 第 45b 页 WYG0799-0587d.png WYG0799-0588a.png

 四率三百七十八石为粮数既得粮数
四率三百七十八石为粮数既得粮数乃以十四石为一率四人为二率三百
七十八石为三率推得四率一百零八
为人数或以九石为一率三人为二率
三百七十八石内减盈五十四石馀三
百二十四石为三率亦得四率一百零
八为人数也盖三十六石与四十二石
互乘皆为支一千五百一十二石然四
十二倍其粮数则盈二千二百六十八
御制数理精蕴 下编卷八 第 45b 页 WYG0799-0587d.png WYG0799-0588a.png

 石三十六倍其粮数则适足三十六倍
石三十六倍其粮数则适足三十六倍御制数理精蕴 下编卷八 第 46a 页 WYG0799-0588c.png
 与四十二倍差六倍知六倍之为二千
与四十二倍差六倍知六倍之为二千二百六十八石即知一倍之为三百七
十八石矣既得粮数则以所支之几石
与几人之比即同于总粮数与总人数
之比也
一朒一适足
设如以车运米每四车载六十石则米少六十石每
三车载四十石则米适足问车数与米数各若干
御制数理精蕴 下编卷八 第 46b 页 WYG0799-0588d.png WYG0799-0589a.png

 法以四车互乘四十石得一百六十石
法以四车互乘四十石得一百六十石以三车互乘六十石得一百八十石相
减馀二十石为一率三车四车互乘得
十二车为二率朒与适足无可加减即
以朒六十石为三率推得四率三十六
为车数既得车数则以十二车为一率
以互乘所得之一百六十石为二率(与/三)
(车为一率四十石为二率同以/其俱为三与四十之比例也)三十六
车为三率推得四率四百八十石为米
御制数理精蕴 下编卷八 第 46b 页 WYG0799-0588d.png WYG0799-0589a.png

 数若将互乘所得之一百八十石为二
数若将互乘所得之一百八十石为二御制数理精蕴 下编卷八 第 47a 页 WYG0799-0589c.png
 率则得四率五百四十石减朒六十石
率则得四率五百四十石减朒六十石亦得四百八十石为米数也此法互乘
后一得十二车载一百八十石一得十
二车载一百六十石其相差为二十石
知二十石为十二车之所差即知六十
石为三十六车之所差故二十石与十
二车之比即同于六十石与三十六车
之比也
御制数理精蕴 下编卷八 第 47b 页 WYG0799-0589d.png WYG0799-0590a.png

 又先得米数之法欲省互乘则将两车
又先得米数之法欲省互乘则将两车数变为同䓁以四车载六十石用四归
三因为三车载四十五石则两首数同
矣乃以四十石与四十五石相减馀五
石为一率四十石为二率朒六十石为
三率推得四率四百八十石为米数既
得米数即以四十石为一率三车为二
率四百八十石为三率推得四率三十
六即车数也此法不用互乘止将两首
御制数理精蕴 下编卷八 第 47b 页 WYG0799-0589d.png WYG0799-0590a.png

 数变为同䓁极为简捷然必其数可以
数变为同䓁极为简捷然必其数可以御制数理精蕴 下编卷八 第 48a 页 WYG0799-0590c.png
 度尽为同等者方可用之若其数不能
度尽为同等者方可用之若其数不能度尽则必仍用互乘之法焉
御制数理精蕴 下编卷八 第 48b 页 WYG0799-0590d.png

御制数理精蕴下编卷八