声明:本站书库内容主要引用自 archive.org,kanripo.org, db.itkc.or.kr 和 zh.wikisource.org
御制数理精蕴 下编卷十四 第 1a 页 WYG0799-0815a.png
 钦定四库全书
钦定四库全书御制数理精蕴下编卷十四
面部四
三角形
御制数理精蕴 下编卷十四 第 2a 页 WYG0799-0816a.png
 三角形
三角形凡三角形立于圆界之一半者为直角即勾股过圆
界之一半者为锐角不及圆界之一半者为钝角然
不拘锐角钝角自一角至底边作垂线即分为两直
角是仍不离乎勾股也两腰等者垂线即当底之一
半而两腰不等者所分底界则有大小不同故和较
相比之法因之而生盖和求较较求和要必归于勾
股相求之理由勾股而得垂线则凡面积及内容方
御制数理精蕴 下编卷十四 第 2b 页 WYG0799-0816b.png WYG0799-0816c.png

 圆等形皆无不可得至于三角形角度相求之法乃
圆等形皆无不可得至于三角形角度相求之法乃割圆八线实所以极三角之用即如周髀所谓仰矩
知高俯矩知深是也故另为一卷兹但取三角形之
面线相求诸法悉具图解以次勾股使与勾股相表
里焉
设如有等边三角形每边十尺求中垂线几何
法以底边十尺折半得五尺为勾任以
两腰之一边十尺为弦勾弦求股得八
尺六寸六分零二毫有馀即为中垂线
御制数理精蕴 下编卷十四 第 2b 页 WYG0799-0816b.png WYG0799-0816c.png

 也如图甲乙丙三角形其甲乙甲丙两
也如图甲乙丙三角形其甲乙甲丙两御制数理精蕴 下编卷十四 第 3a 页 WYG0799-0817a.png
 腰相等则其底边之乙丙两角度亦必
腰相等则其底边之乙丙两角度亦必相等(见几何原夲/二卷第九节)今所求之垂线为甲
丁即将甲乙丙三角形平分为两直角
三角形而甲丁乙甲丁丙皆为直角其
度又等故所分之两直角三角形为同
式形而甲丁垂线又为两三角形所共
用之边线则所分之底边之乙丁丁丙
焉得不等故将乙丙底边折半为勾任
御制数理精蕴 下编卷十四 第 3b 页 WYG0799-0817b.png WYG0799-0817c.png

 以甲乙甲丙两边之一边为弦求得股
以甲乙甲丙两边之一边为弦求得股为中垂线也
又法以底边十尺折半得五尺自乘得
二十五尺三因之得七十五尺开方得
八尺六寸六分零二毫有馀即为中垂
线也盖弦比勾大一倍则弦之自乘之
方必比勾之自乘之方大四倍为连比
例隔一位相加之比例(见几何原夲/七卷第五节)依
勾弦求股之法于弦自乘方积之四倍
御制数理精蕴 下编卷十四 第 3b 页 WYG0799-0817b.png WYG0799-0817c.png

 内减勾自乘方积之一倍馀三倍即为
内减勾自乘方积之一倍馀三倍即为御制数理精蕴 下编卷十四 第 4a 页 WYG0799-0818a.png
 股自乘之方积是中垂线之自乘方积
股自乘之方积是中垂线之自乘方积为勾自乘方积之三倍故将底边折半
自乘三因之即与中垂线自乘之方积
等而开方得中垂线也
设如有锐角三角形大腰一百二十二尺小腰一百
一十二尺底一百五十尺求中垂线几何
法以底一百五十尺为一率大腰一百
二十二尺与小腰一百一十二尺相加
御制数理精蕴 下编卷十四 第 4b 页 WYG0799-0818b.png WYG0799-0818c.png

 得二百三十四尺为二率以大腰一百
得二百三十四尺为二率以大腰一百二十二尺与小腰一百一十二尺相减
馀十尺为三率求得四率十五尺六寸
为底边之较与底一百五十尺相减馀
一百三十四尺四寸折半得六十七尺
二寸为勾以小腰一百一十二尺为弦
求得股八十九尺六寸为中垂线也如
图甲乙丙三角形甲乙为大腰甲丙为
小腰乙丙为底甲丁为所求中垂线试
御制数理精蕴 下编卷十四 第 4b 页 WYG0799-0818b.png WYG0799-0818c.png

 以甲为心丙为界作一圜截甲乙大腰
以甲为心丙为界作一圜截甲乙大腰御制数理精蕴 下编卷十四 第 5a 页 WYG0799-0819a.png
 于庚截乙丙底于戊又将甲乙大腰引
于庚截乙丙底于戊又将甲乙大腰引长至己作甲己线与甲丙小腰相等则
己乙为两腰之和庚乙为两腰之较(盖/甲)
(庚与甲丙等故庚/乙为两腰之较)乙丙为底边之和乙
戊为底边之较(盖丁丙与丁戊等故/乙戊为底边之较)今
以乙丙底边之和与乙己两腰之和为
比即同于乙庚两腰之较与乙戊底边
之较为比为转比例之四率(几何原夲/九卷第八)
御制数理精蕴 下编卷十四 第 5b 页 WYG0799-0819b.png WYG0799-0819c.png

 (节自圜外一点至圜内所作之两线此/两全线之比例同于圜外两段转相比)
(节自圜外一点至圜内所作之两线此/两全线之比例同于圜外两段转相比)(之比/例)故乙丙为一率乙己为二率乙庚
为三率求得四率为乙戊既得乙戊则
于乙丙底边内减去乙戊馀戊丙折半
得丁丙为勾甲丙为弦求为股为甲丁
中垂线也
又法以大腰一百二十二尺自乘得一
万四千八百八十四尺又以小腰一百
一十二尺自乘得一万二千五百四十
御制数理精蕴 下编卷十四 第 5b 页 WYG0799-0819b.png WYG0799-0819c.png

 四尺两自乘数相减馀二千三百四十
四尺两自乘数相减馀二千三百四十御制数理精蕴 下编卷十四 第 6a 页 WYG0799-0820a.png
 尺以底边一百五十尺除之得十五尺
尺以底边一百五十尺除之得十五尺六寸为底边之较与底边一百五十尺
相减馀一百三十四尺四寸折半得六
十七尺二寸为勾以小腰一百一十二
尺为弦求得股八十九尺六寸为中垂
线也如图甲乙丙三角形试自甲角作
甲丁垂线则分为甲丁乙甲丁丙两勾
股形甲乙甲丙皆为弦乙丁丁丙皆为
御制数理精蕴 下编卷十四 第 6b 页 WYG0799-0820b.png WYG0799-0820c.png

 勾共以甲丁为股乙丙为两勾之和乙
勾共以甲丁为股乙丙为两勾之和乙戊为两勾之较今以甲乙弦自乘则成
甲戊己乙一正方形内丁庚辛乙为乙
丁勾自乘之一正方形于甲戊己乙正
方形内减去丁庚辛乙正方形所馀甲
戊己辛庚丁磬折形积即与甲丁股自
乘之一正方形等又以甲丙弦自乘则
成甲壬癸丙一正方形内丁子丑丙为
丁丙勾自乘之一正方形于甲壬癸丙
御制数理精蕴 下编卷十四 第 6b 页 WYG0799-0820b.png WYG0799-0820c.png

 正方形内减去丁子丑丙正方形所馀
正方形内减去丁子丑丙正方形所馀御制数理精蕴 下编卷十四 第 7a 页 WYG0799-0821a.png
 甲壬癸丑子丁磬折形积亦与甲丁股
甲壬癸丑子丁磬折形积亦与甲丁股自乘之一正方形等是则前图之甲戊
己辛庚丁磬折形与后图之甲壬癸丑
子丁磬折形相等矣若两自乘之数相
减则如甲戊己乙正方形内减去与甲
壬癸丑子丁磬折形相等之甲戊己辛
庚丁磬折形又减去丁子丑丙一小正
方形所馀为子庚辛乙丙丑一小磬折
御制数理精蕴 下编卷十四 第 7b 页 WYG0799-0821b.png WYG0799-0821c.png

 形引而长之成一长方形其长即乙丁
形引而长之成一长方形其长即乙丁与丁丙之和其阔即乙丁与丁丙之较
故以乙丁与丁丙之和除子庚辛乙丙
丑磬折形之积而得乙丁与丁丙之较
也又图甲乙丙三角形作甲丁垂线分
为两勾股形共以甲丁垂线为股故甲
乙弦自乘方内有甲丁股自乘一方乙
丁勾自乘一方而甲丙弦自乘方内有
甲丁股自乘一方丁丙勾自乘一方今
御制数理精蕴 下编卷十四 第 7b 页 WYG0799-0821b.png WYG0799-0821c.png

 两勾股形之股既同则两弦方相减所
两勾股形之股既同则两弦方相减所御制数理精蕴 下编卷十四 第 8a 页 WYG0799-0822a.png
 馀之数即两勾方相减所馀之数故甲
馀之数即两勾方相减所馀之数故甲丁乙勾股形之甲乙弦自乘方内减甲
丁丙勾股形之甲丙弦自乘方所馀庚
辛乙寅丑子磬折形即与甲丁乙勾股
形之丁乙勾自乘方内减甲丁丙勾股
形之丁丙勾自乘方所馀乙卯辰己申
未磬折形相等若将乙卯辰己申未磬
折形引而长之遂成乙壬酉未长方形
御制数理精蕴 下编卷十四 第 8b 页 WYG0799-0822b.png WYG0799-0822c.png

 其长即乙丁丁丙两勾之和其阔即乙
其长即乙丁丁丙两勾之和其阔即乙丁丁丙两勾之较其积即乙丁丁丙两
勾方相减之馀亦即甲乙甲丙两弦方
相减之馀是以两弦自乘相减之馀积
以两勾之和除之而得两勾之较也
设如有锐角三角形大腰十七尺小腰十尺底二十
一尺求中垂线几何
法以底二十一尺为一率以大腰十七
尺与小腰十尺相加得二十七尺为二
御制数理精蕴 下编卷十四 第 8b 页 WYG0799-0822b.png WYG0799-0822c.png

 率以大腰十七尺与小腰十尺相减馀
率以大腰十七尺与小腰十尺相减馀御制数理精蕴 下编卷十四 第 9a 页 WYG0799-0823a.png
 七尺为三率求得四率九尺为底边之
七尺为三率求得四率九尺为底边之较与底二十一尺相减馀十二尺折半
得六尺为勾以小腰十尺为弦求得股
八尺为中垂线也如图甲乙丙三角形
甲乙为大腰甲丙为小腰乙丙为底甲
丁为所求中垂线试以甲为心丙为界
作一圜截甲乙大腰于庚截乙丙底边
于戊又将甲乙大腰引长至己作甲己
御制数理精蕴 下编卷十四 第 9b 页 WYG0799-0823b.png WYG0799-0823c.png

 线与甲丙小腰等则己乙为两腰之和
线与甲丙小腰等则己乙为两腰之和庚乙为两腰之较乙丙为底边之和乙
戊为底边之较其乙丙与乙己之比即
同于庚乙与乙戊之比为转比例四率
也
又法以大腰十七尺自乘得二百八十
九尺又以小腰十尺自乘得一百尺两
自乘数相减馀一百八十九尺以底二
十一尺除之得九尺为底边之较与底
御制数理精蕴 下编卷十四 第 9b 页 WYG0799-0823b.png WYG0799-0823c.png

 二十一尺相减馀十二尺折半得六尺
二十一尺相减馀十二尺折半得六尺御制数理精蕴 下编卷十四 第 10a 页 WYG0799-0824a.png
 为勾以小腰十尺为弦求得股八尺为
为勾以小腰十尺为弦求得股八尺为中垂线也图解同前
设如有斜立锐角三角形大腰二十一尺小腰十七
尺底十尺求形外垂线几何
法以底十尺为一率大腰二十一尺与
小腰十七尺相减馀四尺为二率大腰
二十一尺与小腰十七尺相加得三十
八尺为三率求得四率十五尺二寸为
御制数理精蕴 下编卷十四 第 10b 页 WYG0799-0824b.png WYG0799-0824c.png

 底与形外垂线两边连底之总内减去
底与形外垂线两边连底之总内减去底十尺馀五尺二寸折半得二尺六寸
为勾以小腰十七尺为弦求得股十六
尺八尺为形外垂线也如图甲乙丙三
角形甲乙为大腰甲丙为小腰乙丙为
底甲丁为所求形外垂线试以甲为心
丙为界作一圜截甲乙大腰于庚又将
甲乙大腰引长至己作甲己线与甲丙
小腰相等复将乙丙底引长至戊作乙
御制数理精蕴 下编卷十四 第 10b 页 WYG0799-0824b.png WYG0799-0824c.png

 戊线则成甲乙戊三角形其乙丙为底
戊线则成甲乙戊三角形其乙丙为底御制数理精蕴 下编卷十四 第 11a 页 WYG0799-0825a.png
 边之较乙戊为底边之和乙庚为两腰
边之较乙戊为底边之和乙庚为两腰之较乙己为两腰之和自圜外至圜内
所作两线之比例既同于圜外两段转
相比之比例则圜外两段之比例亦必
同于两全线转相比之比例故乙丙与
乙庚之比即同于乙己与乙戊之比为
比例四率既得乙戊则减乙丙馀丙戊
折半得丙丁为勾甲丙为弦求得股即
御制数理精蕴 下编卷十四 第 11b 页 WYG0799-0825b.png WYG0799-0825c.png

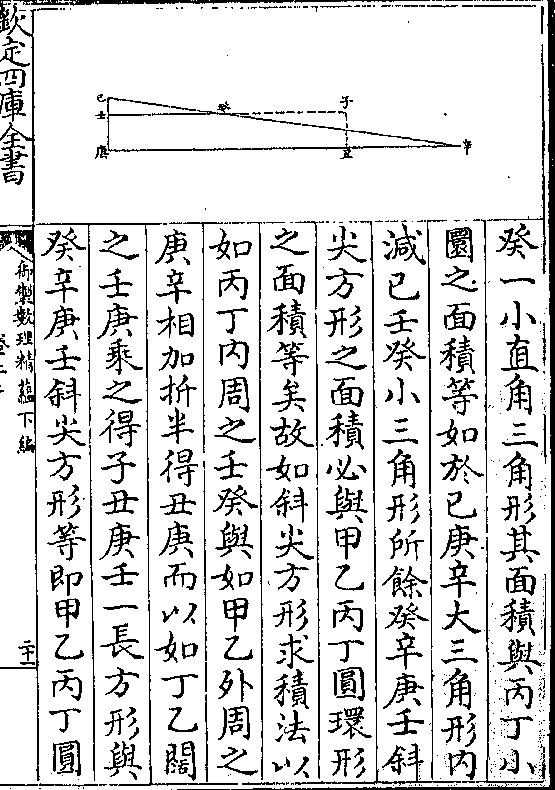 甲丁垂线也
甲丁垂线也又法以大腰二十一尺自乘得四百四
十一尺又以小腰十七尺自乘得二百
八十九尺两自乘数相减馀一百五十
二尺以底十尺除之得十五尺二寸为
底与形外垂线两边连底之总内减底
十尺馀五尺二寸折半得二尺六寸为
勾以小腰十七尺为弦求得股十六尺
八寸为形外垂线也如图甲乙丙三角
御制数理精蕴 下编卷十四 第 11b 页 WYG0799-0825b.png WYG0799-0825c.png

 形将乙丙底引长至戊自甲作垂线至
形将乙丙底引长至戊自甲作垂线至御制数理精蕴 下编卷十四 第 12a 页 WYG0799-0826a.png
 丁则丁戊与丁丙等又自甲至戊作甲
丁则丁戊与丁丙等又自甲至戊作甲戊线与甲丙小腰等则成甲丁乙甲丁
戊两勾股形甲乙甲戊皆为弦乙丁丁
戊皆为勾共以甲丁为股而乙丙为两
勾之较乙戊为两勾之和前法以和求
较此法以较求和其理一也图解并同
前
设如有锐角三角形两腰俱五尺底六尺求面积几
御制数理精蕴 下编卷十四 第 12b 页 WYG0799-0826b.png WYG0799-0826c.png

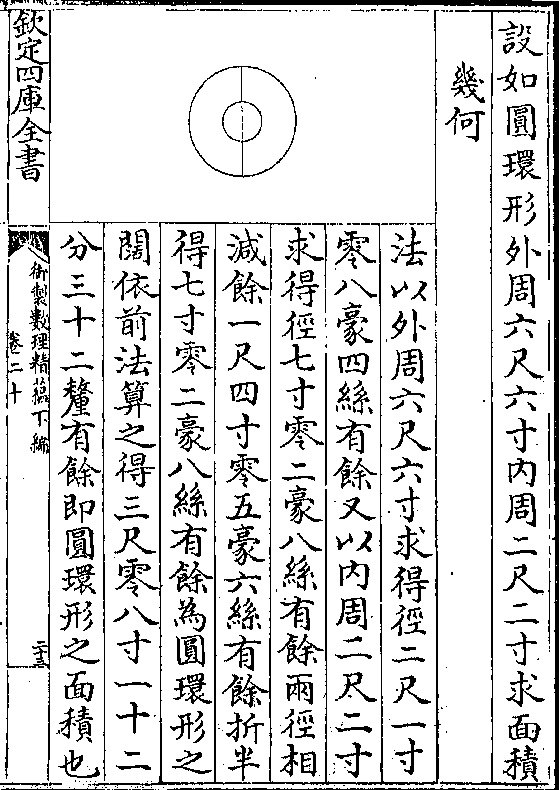 何
何法先以底六尺折半得三尺为勾任以
两腰之一边五尺为弦求得股四尺为
中垂线与底六尺相乘得二十四尺折
半得一十二尺为三角面积也如图甲
乙丙三角形以乙丙底边与甲丁中垂
线相乘成戊乙丙己长方形积比三角
形积正大一倍故折半得三角积也
设如有钝角三角形大腰十七尺小腰十尺底二十
御制数理精蕴 下编卷十四 第 12b 页 WYG0799-0826b.png WYG0799-0826c.png

 一尺求面积几何
一尺求面积几何御制数理精蕴 下编卷十四 第 13a 页 WYG0799-0827a.png
 法先用求中垂线法求得中垂线八尺
法先用求中垂线法求得中垂线八尺与底二十一尺相乘得一百六十八尺
折半得八十四尺为三角面积也如图
甲乙丙三角形先求甲丁垂线既得甲
丁垂线乃与乙丙底边相乘成戊乙丙
己长方形比三角形积正大一倍故折
半得三角积也
又法以甲乙边十七尺乙丙边二十一
御制数理精蕴 下编卷十四 第 13b 页 WYG0799-0827b.png WYG0799-0827c.png

 尺甲丙边十尺三数相加得四十八尺
尺甲丙边十尺三数相加得四十八尺为三边之总折半得二十四尺为半总
以甲乙边十七尺与半总二十四尺相
减馀七尺为甲乙边与半总之较以乙
丙边二十一尺与半总二十四尺相减
馀三尺为乙丙边与半总之较以甲丙
边十尺与半总二十四尺相减馀十四
尺为甲丙边与半总之较乃以半总二
十四尺为一率甲丙边与半总之较十
御制数理精蕴 下编卷十四 第 13b 页 WYG0799-0827b.png WYG0799-0827c.png

 四尺为二率乙丙边与半总之较三尺
四尺为二率乙丙边与半总之较三尺御制数理精蕴 下编卷十四 第 14a 页 WYG0799-0828a.png
 与甲乙边与半总之较七尺相乘得二
与甲乙边与半总之较七尺相乘得二十一尺为三率求得四率十二尺二十
五寸开方得三尺五寸为三角形自中
心至三边之垂线与三边之总四十八
尺相乘得一百六十八尺折半得八十
四尺即三角形之面积或以所得垂线
三尺五寸与半总二十四尺相乘亦得
八十四尺为三角形之面积也此法盖
御制数理精蕴 下编卷十四 第 14b 页 WYG0799-0828b.png WYG0799-0828c.png

 一率二率以线与线为比三率四率以
一率二率以线与线为比三率四率以面与面为比也如甲乙丙三角形自中
心丁至三边各作一垂线又自中心丁
至三角各作一分角线即成六直角三
角形俱两两相等(丁巳丙与丁庚丙等/丁巳乙与丁戊乙等)
(丁戊甲与/丁庚甲等)又按甲戊度引乙丙线至辛
则乙辛为三边之半总即三较之和(乙/巳)
(与乙戊等即甲丙边与半总之较巳丙/与丙庚等即甲乙边与半总之较丙辛)
(与甲戊甲庚等即乙/丙边与半总之较)试自辛作直角将
御制数理精蕴 下编卷十四 第 14b 页 WYG0799-0828b.png WYG0799-0828c.png

 乙丁线引长作一乙辛壬直角形则壬
乙丁线引长作一乙辛壬直角形则壬御制数理精蕴 下编卷十四 第 15a 页 WYG0799-0829a.png
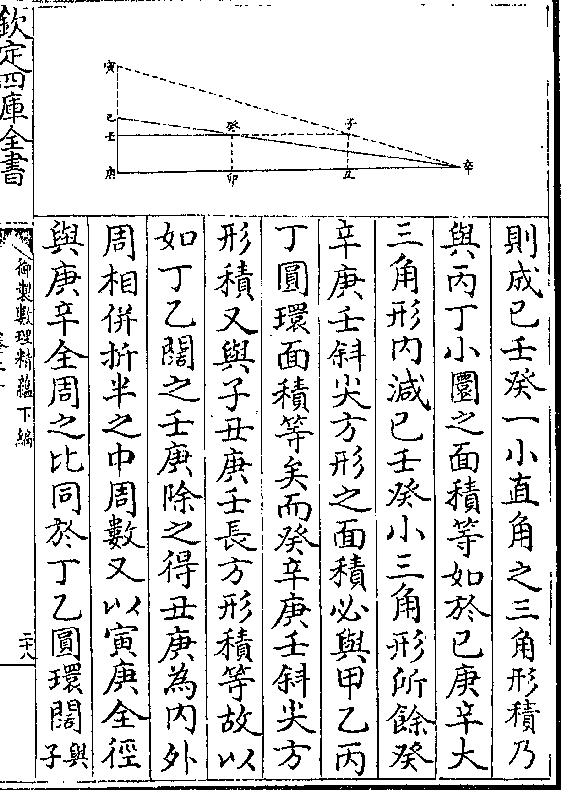 辛与丁巳平行乙辛壬形与乙巳丁形
辛与丁巳平行乙辛壬形与乙巳丁形遂为同式形其乙辛与乙巳之比即同
于壬辛与丁巳之比然乙辛一率乙巳
二率之数虽有而壬辛之数却无又但
知巳丙与丙辛相乘之数即丁巳与壬
辛相乘之数故以巳丙与丙辛相乘之
数为三率(何以知巳丙与丙辛相乘之/数即丁巳与壬辛相乘之数)
(试作壬丙线壬癸线使丙癸与丙辛等/癸角辛角皆为直角癸丙辛角与辛壬)
御制数理精蕴 下编卷十四 第 15b 页 WYG0799-0829b.png WYG0799-0829c.png

 (癸角相合共成一百八十度然庚丙巳/角为癸丙辛角之外角相合亦共成一)
(癸角相合共成一百八十度然庚丙巳/角为癸丙辛角之外角相合亦共成一)(百八十度是庚丙巳角与辛壬癸角等/庚丁巳角与癸丙辛角等是以壬癸丙)
(辛形与丙庚丁巳形为同式形而丙辛/壬勾股形与丁己丙勾股形亦为同式)
(形可互相比例矣以丁己作一率巳丙/作二率丙辛作三率即得四率壬辛是)
(以巳丙二率与丙辛三率相乘之数即/与丁巳一率与壬辛四率相乘之数等)
(故直以己丙丙辛相/乘之数作三率也)其所得四率即丁
己自乘之数是故乙辛与乙巳之比同
于丁己与壬辛相乘之面(即己丙与丙/辛相乘之面)
与丁己自乘之面之比也既得丁己自
御制数理精蕴 下编卷十四 第 15b 页 WYG0799-0829b.png WYG0799-0829c.png

 乘之面故开方而得丁巳为三角形自
乘之面故开方而得丁巳为三角形自御制数理精蕴 下编卷十四 第 16a 页 WYG0799-0830a.png
 中心至三边之垂线与丁戊丁庚俱相
中心至三边之垂线与丁戊丁庚俱相等又即三角形容圜之半径也既得自
中心至三边之垂线则用垂线与三边
之总相乘所得一长方积(即如用垂线/与三边各相)
(乘所得三长方/积合为一长方)比三角形积大一倍故
折半而得三角形之面积如以垂线与
半总相乘即与三角形积等而不用折
半矣
御制数理精蕴 下编卷十四 第 16b 页 WYG0799-0830b.png WYG0799-0830c.png

 设如有锐角三角形大腰三十七尺小腰十五尺底
设如有锐角三角形大腰三十七尺小腰十五尺底四十四尺求内容正方边几何
法先用求中垂线法求得中垂线十二
尺与底边四十四尺相加得五十六尺
为一率中垂线十二尺为二率底边四
十四尺为三率推得四率九尺四寸二
分八釐五毫有馀即三角形内所容正
方之一边也如图甲乙丙三角形甲乙
为大腰甲丙为小腰乙丙为底甲丁为
御制数理精蕴 下编卷十四 第 16b 页 WYG0799-0830b.png WYG0799-0830c.png

 所得中垂线戊己庚辛为今所求内容
所得中垂线戊己庚辛为今所求内容御制数理精蕴 下编卷十四 第 17a 页 WYG0799-0831a.png
 正方形试依甲丁中垂线度将乙丙线
正方形试依甲丁中垂线度将乙丙线引长作乙癸线为五十六尺又与甲丙
线平行作壬癸线又将甲乙线引长作
壬乙线则成与甲乙丙同式之壬乙癸
三角形复与底线平行作甲子线与丙
癸等即与甲丁垂线等又与甲丁平行
作子丑线与甲丁等则甲丁垂线所作
甲丁丑子正方形即为壬乙癸三角形
御制数理精蕴 下编卷十四 第 17b 页 WYG0799-0831b.png WYG0799-0831c.png

 内所容之正方形矣故壬乙癸三角形
内所容之正方形矣故壬乙癸三角形之乙癸底与甲丁方边之比即同于甲
乙丙三角形之乙丙底与戊巳方边之
比故中垂线与底边相加为一率中垂
线为二率底边为三率推得四率为内
容正方之一边也
设如等边三角形每边一尺二寸求内容圜径几何
法先用求中垂线法求得中垂线一尺
零三分九釐二毫有馀以三归之得三
御制数理精蕴 下编卷十四 第 17b 页 WYG0799-0831b.png WYG0799-0831c.png

 寸四分六釐四毫有馀即内容圜形半
寸四分六釐四毫有馀即内容圜形半御制数理精蕴 下编卷十四 第 18a 页 WYG0799-0832a.png
 径倍之得六寸九分二釐八毫有馀即
径倍之得六寸九分二釐八毫有馀即内容圜形全径也如图甲乙丙三角形
内容丁圜形先求得甲戊中垂线又自
丙角至甲乙线界作丙巳垂线与甲戊
中垂线相交于丁即三角形之中心亦
即内容圜形之中心故丁戊与丁己即
内容圜形之半径又甲戊乙甲巳丁两
勾股形为同式形甲乙为乙戊之二倍
御制数理精蕴 下编卷十四 第 18b 页 WYG0799-0832b.png WYG0799-0832c.png

 则甲丁亦必为丁巳或丁戊之二倍丁
则甲丁亦必为丁巳或丁戊之二倍丁戊既为内容圜形之半径则甲丁即为
内容圜形之全径而甲戊中垂线必为
丁戊半径之三倍矣故求得甲戊中垂
线以三归之得丁戊即内容圜形之半
径倍之得庚戊即内容圜形之全径也
设如等边三角形每边一尺二寸求外切圜径几何
法先用求中垂线法求得中垂线一尺
零三分九釐二毫有馀三归四因得一
御制数理精蕴 下编卷十四 第 18b 页 WYG0799-0832b.png WYG0799-0832c.png

 尺三寸八分五釐六毫有馀即外切圜
尺三寸八分五釐六毫有馀即外切圜御制数理精蕴 下编卷十四 第 19a 页 WYG0799-0833a.png
 形全径也如图甲乙丙三角形外切丁
形全径也如图甲乙丙三角形外切丁圜形先求得甲戊中垂线又自丙角至
甲乙线界作丙己垂线与甲戊中垂线
相交于丁即三角形之中心亦即外切
圜形之中心故甲丁与丙丁即外切圜
形之半径又甲戊乙甲巳丁两勾股形
为同式形甲乙为乙戊之二倍则甲丁
亦必为丁己或丁戊之二倍甲丁既为
御制数理精蕴 下编卷十四 第 19b 页 WYG0799-0833b.png WYG0799-0833c.png

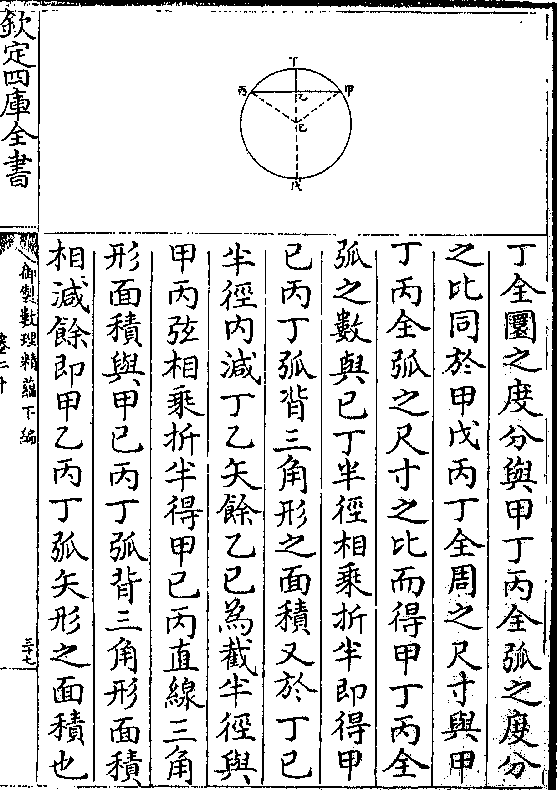 外切圜形之半径则为甲戊中垂线之
外切圜形之半径则为甲戊中垂线之三分之二而甲戊中垂线却为甲庚全
径之四分之三矣故求得甲戊中垂线
三归四因得甲庚即外切圜形之全径
也
又法以每边一尺二寸自乘三归四因
开方得一尺三寸八分五釐六毫有馀
即外切圜形全径也如图甲乙丙三角
形外切甲乙丁丙圜形试自甲角作甲
御制数理精蕴 下编卷十四 第 19b 页 WYG0799-0833b.png WYG0799-0833c.png

 戊中垂线又引长作甲丁全径线复自
戊中垂线又引长作甲丁全径线复自御制数理精蕴 下编卷十四 第 20a 页 WYG0799-0834a.png
 丁至乙作丁乙线遂成甲乙丁甲戊乙
丁至乙作丁乙线遂成甲乙丁甲戊乙两勾股形为同式形甲乙既为乙戊之
二倍则甲丁亦必为乙丁之二倍故甲
丁自乘方积比乙丁自乘方积大四倍
若依勾弦求股之法言之则甲丁弦自
乘方积内减乙丁勾自乘方积所馀为
甲乙股自乘之方积今甲丁弦自乘方
积既为乙丁勾自乘方积之四倍则是
御制数理精蕴 下编卷十四 第 20b 页 WYG0799-0834b.png WYG0799-0834c.png

 甲乙每边自乘方积为甲丁全径自乘
甲乙每边自乘方积为甲丁全径自乘方积之四分之三矣故以一边自乘三
归四因即与全径自乘之方积等而开
方得外切圜形之全径也
设如有锐角三角形大腰三百三十八尺小腰三百
尺底四百一十八尺求内容圜径几何
法先用求中垂线法求得中垂线二百
四十尺与底四百一十八尺相乘得一
十万零三百二十尺以大腰三百三十
御制数理精蕴 下编卷十四 第 20b 页 WYG0799-0834b.png WYG0799-0834c.png

 八尺小腰三百尺底四百一十八尺三
八尺小腰三百尺底四百一十八尺三御制数理精蕴 下编卷十四 第 21a 页 WYG0799-0835a.png
 数相加得一千零五十六尺除之得九
数相加得一千零五十六尺除之得九十五尺即内容圜半径倍之得一百九
十尺即内容圜全径也如图甲乙丙三
角形内容戊圜形试自圜之中心至甲
乙丙三角各作戊甲戊乙戊丙三线遂
分甲乙丙三角形为甲戊乙甲戊丙乙
戊丙三三角形其三边皆为三角形之
底而戊巳半径皆为三角形之垂线今
御制数理精蕴 下编卷十四 第 21b 页 WYG0799-0835b.png WYG0799-0835c.png

 乙丙底边与甲丁中垂线相乘所得之
乙丙底边与甲丁中垂线相乘所得之长方积原比甲乙丙三角形积大一倍
即如将所分三三角形各用垂线乘底
边所得之三长方积合为一长方也三
长方之长虽不同而阔则一故各以长
除积而得阔者即如合三角形之三边
除三角形之倍积而得半径也
设如有锐角三角形大腰一百八十三尺小腰一百
六十八尺底二百二十五尺求外切圜径几何
御制数理精蕴 下编卷十四 第 21b 页 WYG0799-0835b.png WYG0799-0835c.png

 法用求中垂线法求得中垂线一百三
法用求中垂线法求得中垂线一百三御制数理精蕴 下编卷十四 第 22a 页 WYG0799-0836a.png
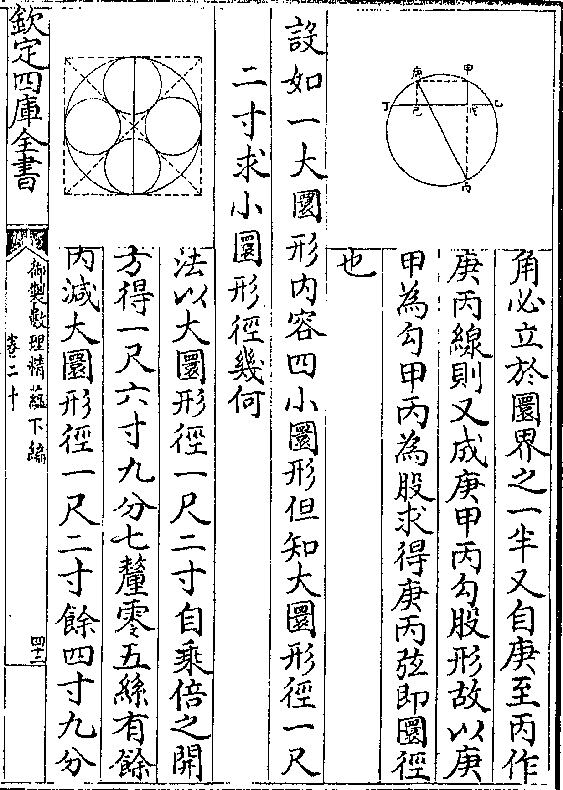 十四尺四寸为一率小腰一百六十八
十四尺四寸为一率小腰一百六十八尺为二率大腰一百八十三尺为三率
推得四率二百二十八尺七寸五分即
外切圜径也如图甲乙丙三角形甲乙
为小腰甲丙为大腰乙丙为底甲丁为
中垂线试作切三角一圜自甲角至圜
对界作甲戊全径线又自丙角至戊作
丙戊线则甲丙戊三角形之丙角立于
御制数理精蕴 下编卷十四 第 22b 页 WYG0799-0836b.png WYG0799-0836c.png

 圜界之一半必为直角与甲丁垂线所
圜界之一半必为直角与甲丁垂线所分甲丁乙三角形之丁角等而戊角与
乙角皆对甲丙弧其度又等故甲丙戊
与甲丁乙两三角形为同式形是以甲
丁与甲乙之比同于甲丙与甲戊之比
而为相当比例四率也
设如有钝角三角形大腰十七尺小腰十尺底二十
一尺求外切圜径几何
法用求中垂线法求得中垂线八尺为
御制数理精蕴 下编卷十四 第 22b 页 WYG0799-0836b.png WYG0799-0836c.png

 一率小腰十尺为二率大腰十七尺为
一率小腰十尺为二率大腰十七尺为御制数理精蕴 下编卷十四 第 23a 页 WYG0799-0837a.png
 三率推得四率二十一尺二寸五分即
三率推得四率二十一尺二寸五分即外切圜径也如图甲乙丙三角形甲乙
为小腰甲丙为大腰乙丙为底甲丁为
中垂线试作切三角一圜自甲角至圜
对界作甲戊全径线又自丙角至戊作
丙戊线则甲丙戊三角形之丙角立于
圜界之一半必为直角与甲丁垂线所
分甲丁乙三角形之丁角等而戊角与
御制数理精蕴 下编卷十四 第 23b 页 WYG0799-0837b.png WYG0799-0837c.png

 乙角皆对甲丙弧其度又等故甲丙戊
乙角皆对甲丙弧其度又等故甲丙戊与甲丁乙两三角形为同式形是以甲
丁与甲乙之比同于甲丙与甲戊之比
而为相当比例四率也
御制数理精蕴 下编卷十四 第 23b 页 WYG0799-0837b.png WYG0799-0837c.png

 御数精蕴下编卷十四
御数精蕴下编卷十四