钦定古今图书集成.历象汇编.历法典.测量部
钦定古今图书集成历象汇编历法典
第一百三卷目录
测量部汇考四
诗经〈鄘风定之方中 大雅公刘〉
易纬〈通卦验〉
书纬〈考灵曜〉
淮南子〈天文训〉
隋书〈天文志〉
宋史〈律历志〉
宣和博古图〈周双螭表座 汉表座〉
元史〈天文志〉
新法历书一〈大测上〉
诗经〈鄘风定之方中 大雅公刘〉
易纬〈通卦验〉
书纬〈考灵曜〉
淮南子〈天文训〉
隋书〈天文志〉
宋史〈律历志〉
宣和博古图〈周双螭表座 汉表座〉
元史〈天文志〉
新法历书一〈大测上〉
历法典第一百三卷
测量部汇考四
《诗经》鄘风定之方中
定之方中,作于楚宫。揆之以日,作于楚室。〈传〉定,营室也。揆,度也。度日出日入以知东西,南视定北准极以正南北。室,犹宫也。〈笺〉定星昏中而正,于是可以营制宫室,故谓之营室。定昏中而正,谓小雪时,其体与东壁连正四方。〈疏〉《正义》曰:此度日出日入,谓度其影也。故《公刘传》曰:考于日影是也。其术则匠人云水地以县,置槷以悬视,以影为规,识日出之影,与日入之影。昼参诸日中之影,夜考之极星,以正朝夕。注云:于四角立植而悬以水,望其高下。高下既定,乃为位而平也。于所平之地中央树八尺之槷以悬正之视之以其影端,以至日入既则为规。测影两端之内规之,规之交乃其审也。度两交之间,中屈之以指槷,则南北正也,日中之影最短者也。极星谓北辰也,是揆日瞻星,以正东西南北之事也。如匠人注:度日出日入之影,不假于视,定视极而东西南北皆知之。此传度日出入以知东西,视定极以正南北者,考工之文,止言以正朝夕,无正南北之语。故规影之下,别言考之,极星是视,极乃南北正矣。但郑因屈横度之绳,即可以知南北,故细言之,与此不为乖也。
大雅公刘
笃公刘,既溥既长,既景乃冈。相其阴阳,观其流泉。〈传〉既景,乃冈考于日景,参之高冈。〈笺〉以日景定其经界于山之脊观,相其阴阳寒煖所宜,流泉浸润所及,皆为利民富国。〈疏〉日影定其经界者,民居田亩,或南或东,皆须正其方面,故以日影定之。
《易纬》通卦验
冬至之日,树八尺之表。日中视其晷景长短,以占和否。夏至影一尺四寸八分,冬至一丈三尺。《书纬》考灵曜
日末影尺五寸,日短景尺三寸。《淮南子》天文训
正朝夕,先树一表东方,操一表却去前表十步以参望。日始出,北廉日直入。又树一表于东方,因西方之表以参望,日方入北廉,则定东方。两表之中与西方之表则东西之正也。日冬至,日出东南,维入西南。维至春秋分,日出东中入西中。夏至出东北,维入西北。维至则正南。欲知东西南北广袤之数者,立四表以为方一里距先春分若秋分十馀日。从距北表参望,日始出及旦以候相应,相应则此与日直也。辄以南表参望之,以入前表数为法。除举广,除立表。袤以知从,此东西之数也。假使视日出入,前表中一寸,是寸得一里也。一里积万八千寸得从,此东万八千里。视日方入,入前表半寸,则半寸得一里。半寸而除一里,积寸得三万六千里。除则从此,西里数也,并之东西里数也,则极径也,未春分而直,已秋分而不直,此处南也。未秋分而直,已春分而不直,此处北也。分至而直,此处南北中也。从中处欲知中南也,未秋分而不直,此处南北中也。从中处欲知南北,极远近从西南表参望日。日夏至始出,与北表参则是东。与东北表等,正东万八千里则从中,北亦万八千里也。倍之南北之里数也,其不从中之数也。以出入前表之数益损之。表入一寸,寸减日近一里;表出一寸,寸益远一里。欲知天之高,树表高一丈,正南北,相去千里同日度其阴,北表二尺,南表尺九寸,是南千里阴短寸,南二万里则无景,是直日下也。阴二尺而得高一丈者,南一而高五也。则置从此南至日下里数,因而五之为十万里,则天高也。若使景与表等,则高与远等也。《隋书》天文志
《周礼》:大司徒职,以土圭之法测土深,正日景以求地中,此则浑天之正说,立仪象之大本。故云:日南则景短,多暑;日北则景长,多寒;日东则景夕多风,日西则景朝多阴。日至之景,尺有五寸,谓之地中,天地之所合也,四时之所交也,风雨之所会也,阴阳之所和也。然则百物阜安乃建王国焉。又考工记匠人建国水地以县置槷,以县视。以景为规,识日出之景与日入之景。昼参诸日中之影,夜考之极星以正朝夕。按:土圭正影,经文阙略,先儒解说,又非明审。祖暅错综经注以推地中,其法曰:先验昏旦,定刻漏,分辰次,乃立仪表于准平之地,名曰南表。漏刻上水居日之中,更立一表于南,表影末,名曰中表。夜依中表以望北极枢而立北表,令参相直。三表皆以县准定乃观,三表直者,其立表之地,即当子午之正。三表曲者,地偏僻。每观中表以知所偏,中表在西,则立表处在地中之西,当更向东求地中。若中表在东,则立表处在地中之东也,当更向西求地中。取三表直者为地中之正。又以春秋二分之日,旦始出东方半体,乃立表于中表之东,名曰东表。令东表与日及中表参相直,是日之夕。日入西方半体,又立表于中表之西,名曰西表。亦从中表西望西表。及日参相直,乃观三表直者,即地南北之中也。若中表差近南,则所测之地在卯酉之南。中表差在北,则所测之地在卯酉之北。进退南北求三表直,正东西者则其地处中,居卯酉之正也。〈地中〉昔者周公测晷景于阳城,以参考历纪。其于周礼,在大司徒之职,以土圭之法测土深,正日景以求地中。日至之景,尺有五寸,则天地之所合,四时之所交,百物阜安乃建王国。然则日为阳精元象之著然者也。生灵因之动息,寒暑由其递代。观阴阳之升降,揆天地之高远。正位辨方,定时考闰,莫近于兹也。古法简略,旨趣难究。术家考测,互有异同。先儒皆云:夏至立八尺表于阳城,其影与土圭等。案《尚书·考灵曜》称,日永景尺五寸,日短景尺三寸。《易通卦验》曰:冬至之日,树八尺之表,日中视其晷景长短以占和否。夏至景一尺四寸八分,冬至一丈三尺。《周髀》云:成周土中夏至景一尺六寸,冬至景一丈三尺五寸。刘向《鸿范传》曰:夏至景长一尺五寸八分,冬至一丈三尺一寸四分,春秋二分景七尺三寸六分。后汉《四分历》、魏《景初历》、宋《元嘉历》、《大明祖冲之历》皆与《考灵曜》同。汉魏及宋所都,皆别四家历法。候景则齐,且纬候所陈,恐难依据。刘向二分之景直以率推,非因表候定其长短。然寻晷景尺丈,虽有大较,或地域不改而分寸参差,或南北殊方而长短维一。盖术士未能精验,冯古所以致乖。今删其繁杂,附于此云:梁天监中、祖暅造八尺铜表,其下与圭相连。圭上为沟,置水以取平,正揆测日晷求其盈缩。至大同十年,太史令虞𠠎又用九尺表格,江左之景夏至一尺三寸二分,冬至一丈三尺七分。立夏、立秋二尺四寸五分,春分、秋分五尺三寸九分。陈氏一代,唯用梁法。齐神武以洛阳旧器,并徙邺中以暨。文宣受终,竟未考验。至武平七年,讫于景礼。始荐刘孝孙、张孟宾等于后主刘张建表,测景以考分至之气,草创未就,仍遇朝亡。周自天和以来,言历者纷纷复出,亦验二至之景以考历之精粗。及高祖践极之后,大议造历。张胄元兼明揆测言:日长之瑞有诏司,存而莫能考决。至开皇十九年,袁充为太史令,欲成胄元旧事,复表曰:隋兴已后,日景渐长。开皇元年冬至之景长一丈二尺七寸二分,自尔渐短。至十七年,冬至景一丈二尺六寸三分。四年冬至,在洛阳测景长一丈二尺八寸八分,二年夏至景一尺四寸八分,自尔渐短。至十六年夏至景一尺四寸五分,其十八年冬至阴云,不测。元年十七年、十八年亦阴云,不测。周官以土圭之法正日景,日至之景尺有五寸。郑元云:冬至之景一丈三尺,今十六年夏至之景短于旧五分。十七年冬至之景短于旧三寸七分。日去极近则景短,而日长去极远则景长。而日短行内道则去极近,行外道则去极远。《尧典》云:日短星昴以正仲冬据昴星昏中,则知尧时仲冬日在须女十度。以历数推之,开皇以来冬至日在斗十一度,与唐尧之代去极俱近。谨案《元命包》云:日月出内道,璇玑得其常。天帝崇灵圣王,初功京房别对曰:太平日行上道升平,日行次道霸代,日行下道伏惟。大隋启运上感乾元景短日长,振古希有是。时废庶人勇晋王广初为太子,充奏此事,深合时宜。上临朝谓百官曰:景长之庆,天之祐也。今太子新立,当须改元,宜取日长之意以为年号。由是改开皇二十一年为仁寿元年。此后百工作役,并加程课,以日长故也。皇太子率百官诣阙,陈贺案日徐疾盈缩无常,充等以为祥瑞,大为议者所贬。又《考灵曜》、《周髀》、张衡《灵宪》及郑元《注周官》并云:日影于地千里而差一寸。案宋元嘉十九年,壬午使使往交州测影,夏至之日影出表南三寸二分。何承天遥取阳城云:夏至一尺五寸。计阳城去交州路当万里,而影实差一尺八寸二分,是六百里而差一寸也。又梁大同中,二至所测以八尺表率取之,夏至当一尺一寸七分彊。后魏信都芳注周髀四术称,永平元年戊子,当梁天监之七年,见洛阳测影又见。公孙崇集诸朝士共观,秘书影同是。夏至日其中影皆长一尺五寸八分。以此推之,金陵去淮南北略当千里而影差四寸,则二百五十里而影差一寸也。况人路迂回,山川登降,方于鸟道所校弥多,则千里之言未足依也。其揆测参差如此,故备论之。〈晷影〉
《宋史》律历志
英宗明天历法,升降分:皇极躔衰有陟降率,麟德以日景差、陟降率、日晷景消息为之,义通轨漏。夫南至之后,日行渐升,去极近,故晷短而万物皆盛;北至之后,日行渐降,去极远,故晷长而万物寖衰。自大衍以下,皆从麟德。今历消息日行之升降,积而为盈缩焉。岳台日晷,岳台者,今京师岳台坊地曰浚仪近古候景之所,《尚书·洛诰》称东土是也。《礼·玉人职》土圭长尺有五寸以致日,此即日有常数也。司徒职以圭正日晷,日至之景尺有五寸,谓之地中,此即是地土中,致日景与土圭等。然表长八尺,见于《周髀》。夫天有常运,地有常中,历有正象,表有定数。言日至者,明其日至此也。景尺有五寸与圭等者,是其景晷之真效然。夏至之日尺有五寸之景,不因八尺之表,将何以得。故经见夏至日景者,明表有定数也。【宣和博古图】
&&图表=340151a【周双螭表座】
&&图表=340151b右表座高一尺三寸七分,下径一尺九寸三分,重五十五斤。无铭。周官置槷昼以参诸日中之景。槷即表也。是器形若大盘,上蟠双螭,而仰其首于两螭间。又出一筒,中通上下,是为表座中通。所以植槷无欹,侧以取其端焉。
【汉表座】
&&图表=340151c右表座高四寸六分,深四寸二分,阔七寸一分,口径一寸一分,重三斤九两。无铭。是器,表座也。作三圜筒相合为一体,措之地则一筒端立可以立表。周官所谓槷者,是器所以为测日之具也。
《元史》天文志
鲁哈麻亦渺凹只,汉言春秋分晷影堂。为屋二间,脊开东西横罅,以斜通日晷。中有台,随晷影南高北下,上仰置铜半环,刻天度一百八十,以准地上之半天,斜倚锐首铜尺,长六尺,阔一寸六分,上结半环之中,下加半环之上,可以往来窥运,侧望漏屋晷影,验度数,以定春秋二分。鲁哈麻亦木思塔馀,汉言冬夏至晷影堂也。为屋五间,屋下为坎,深二丈二尺,脊开南北一罅,以直通日晷。随罅立壁,附壁悬铜尺,长一丈六尺。壁仰画天度半规,其尺亦可往来规运,直望漏屋晷影,以定冬夏二至。《新法历书一》大测上
大测者,测三角形法也。凡测算皆以此测彼。而此一彼一不可得。测九章算多以三测,一独句股章以二测。一则皆三角形也,其不言句股者,句与股交必为直角。直角者,正方角也,遇斜角则句股穷矣。分斜角为两直角,亦句股也。遇或不可得分,又穷矣。三角形之理,非句股可尽,故不名句股也。句股之易测者,直线也,平面也。测天则圜面曲线,非句股所能得也。故有弧矢弦割圜之法。弧者,曲线。弦矢者,直线也。以弧求弧无法可得,必以直线曲弧相当相准,乃可得之。相当相准者,围径之法也。而围与径终古,无相准之率。古云:径一围,三实围以内。二径之六弦,非围也。祖冲之密率云:径七围二十二,则其外切线也,非围也。刘徽密率云:径五十围百五十七,则又其内弦也,非围也。或推至万万亿以上然。而小损即内弦,小益即外切线也,终非围也。历家以句股开方,展转商求,累时方成一率。然不能离径一围三之法,即祖率已繁,不复能用,况徽率乎。况万万亿以上乎。是以甚难而实谬。今西法以周天一象限分为半弧,而各取其正半弦。其术从二径六弦,始以次求得六宗率皆度数之正义无可疑者。次用三要法相分相准,以求各率,而得各弧之正半弦。又以其馀弧之正弦为馀弦,以馀弦减半径为矢弧之外,与正弦平行而,交于割线者,为切线。以他半径截弧之一端而交于切线者,为割线。其与馀弦平行者,则馀切线也。即正割一线交于馀切线,而止者,馀割线也。以正弦减半径者,馀矢也。总之为八线,其弧度分为五千四百。每一度分有八线焉,合之为四万三千二百率也。其用之则一形中有三边、三角,任有其三可得其馀三也。凡测候所得者,皆弧度分也。以此二三弧求彼一弧,先简此弧之某直线与彼弧之某直线,推算得数简表,即得彼弧之度分。不劳馀力,不费晷刻。为之者,劳用之者,逸方之句股。开方以测圆者,甚易而实是也。然则必无差乎。曰:有之。或在其末位。如半径设十万,则所差者,十万分之一也。设千万则所差者,千万分之一也。历家推演至微,纤以下率皆弃去,即谓之无差亦可。故论此法者,谓于推步术中为模范矣。测天者,所必须大于他测,故名大测,其解义六篇,谨列如左:因明篇第一
总论〈凡三十二条〉
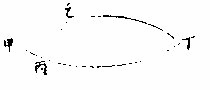
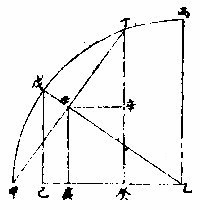
三角形者,一形而三边。容有三角也。如左图:甲乙丙
图
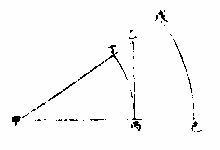
为平面三角形,丁戊己为球面三角形。
三角形各以两边容一角,此两边为角形之两腰,第三边为角形之底。
如上:甲乙丙形,若以甲乙甲丙为两腰,则容乙甲丙角,〈第二字为所指角〉乙丙其底也,馀二同,丁戊己亦同。
图

各边向一角者,名为对角。如上甲乙线向丙角者,名为对丙角,甲丙向乙名为对乙角。
角以何为尺度。一弧之心在交点,从心引出线为两腰,而弧在两腰之间,此弧即此角之尺度。
如上乙甲丙角,其尺度则
图

丁丙或戊己皆是。其法甲为心其界或近如丁丙,或远如戊己。
大测法:分圈三百六十为度,度析百分,〈中历〉或六十分,〈远西〉分或百析为秒,递析为百至纤而止。〈中历〉或析为六十秒,递析为六十至十位而止。〈远西〉
圈愈大,其度分亦愈大。两弧之分数等,其圈等弧亦等。其圈不等,弧亦不等。其不等之两弧,名相似弧。如上丁丙虽小于戊己,而同对甲角,即同为若干度分之弧也。
圈四分之一为九十度,有弧不足九十度,则其外
图
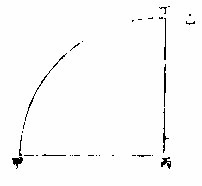
至九十者,名馀弧,亦曰较弧,亦曰差弧。
如甲丁弧四十度,则丁至丙五十度为馀弧。
有弧大于象限,〈在九十以上〉名为过弧。
如甲乙弧大于甲丁,过九十度则丁乙为过弧。半圈界一百八十度,有弧小于半圈,则其外至百八十度者,名为半圈之较弧。
如甲乙弧小于甲乙丙半圈,则乙丙为其较弧。凡交角俱相等。
如甲与乙,丙与丁,皆交角相等。〈见几何第一卷十五题〉如戊与己亦交角相等。
图

角有二类:一直角,一斜角。凡直角其度皆九十。斜角有二类:一锐角,一钝角。
钝角者,其度大于象限。锐角者,其度小于象限。角之馀,与弧同理。〈或曰较角或曰差角〉
有两角并在一线,上为同
方,角并之等于两直角。如右图甲与乙,丙与丁皆是同方,两角等于两直角,故彼角为此角之较。
如前乙角即甲之较,甲亦乙之较。
三角形或三边等,或两边等,或三不等。
三角形两腰等,其底线上两角亦等。底上两角等,则两腰亦等。〈见几何一卷第五〉
三边形之三角等,则三边亦等。
三角形之角有二类:一为直角三边形,一为斜角三边形。
直角三边形,形内止有一直角。
直角三边形之对直角边名弦,两腰名句股。
远西句股,俱各垂线互用之。
斜角形其角皆斜。
斜角形有二类:一曰锐角,一曰钝角。
钝角形止有一钝角。
锐角形三皆锐角。
三角形有二类:一曰平面上形,一曰球上形。
论平面上三角形〈凡十一条〉
平面上三角形有三种:一直线,一曲线,一杂线。大测所论皆直线也。
凡等角,两三边形其在等角旁之各两腰线相与为比例必等。而对等角之边为相似边。〈几何六卷第四题〉凡两三角形其角两边之比例等,即两形为等角形。而对各相似边之角各等。〈几何六卷第五题〉
此二题为大测之根本,不用开方,直以比例得之。法至简,用至大也。
如左图甲乙丙、丁戊己两形,甲与丁,乙与戊,丙与己
图

皆等角,其旁各两腰之比例等者,十与六若五与三也。更之,则十与五若六与三也。反之,则六与十若三与五也。
凡两形中,各对相当等角之边皆相似之边。如甲丙对乙,丁己对戊。而乙戊为等角者,即甲丙丁己为相似之边也。
三角形之外角与相对之内两角并等。〈几何一卷之三十二〉如上甲乙丙形之乙甲两角并,与甲丙丁角等。三角形之三角并,等于两直角。
如上图丁己庚直角与乙角等,其甲丙二角并与丁
图
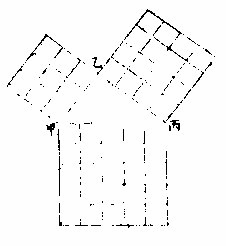
己戊角等。
平面上三角形止有一直角或一钝角,其馀二必皆锐角。
三边形内之第三角为前两角之馀角,何者。为前两角不满二直角故。
直角旁之两腰,其能与弦等。能等者谓两腰,上两方
图
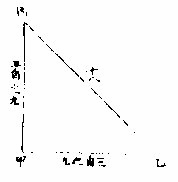
形并与弦上方形等也。〈几何一卷之四七〉
此理之用为:先得二边以求第三边。如甲乙丙形先得甲乙、乙丙两边,而求第三边法:以甲乙三自之为九,乙丙四自之为十六,并得二十五,与甲丙之实等。开方得甲丙弦五。若先得
图
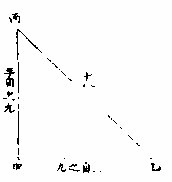
直角旁之一腰,如甲乙三,又得甲丙弦五,而求乙丙。则以甲丙自之得二十五,乙甲自之得九,相减之较十六,开方得乙丙四。直角形之两等边有数,则其弦无数,可推。若弦有数,则两等边无数,可推。如图甲乙、甲丙各三自之
图
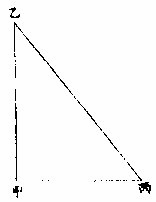
各九,并之得十八。乙丙上实十八,开方得四,馀实二分之,或为八分之二或为九分之二。八分之二则大于真率,九分之二则小于真率。其乙丙真率无数可得更细分之,亦复不尽。直角三边形之两锐角,彼锐为此锐之馀。
图
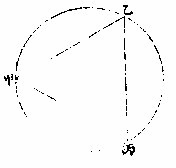
如乙丙二锐角,丙为馀角,为三角并等二直角。此二锐应等一直角,乙一角不足一直角,故丙角为乙角与直角相减之较。
平边三角形在圈内,其各角之度数皆为其对弧度数之半。
如上甲乙丙形三边等分
图
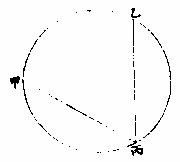
圈为三,各弧俱一百二十度。本形之三角等二直角,并得一百八十。则对弧百二十度倍于对角六十度也。
平面两三角形在圈内,同底两形之顶相连成一四边形。此形内有两对角线,则此形相对之各两边,各
图
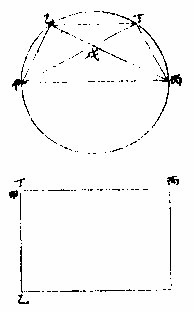
相偕为两直角,形并与两对角线相偕为直角形等。如上甲乙丙、甲丁丙两三角形在甲乙丁丙圈内,甲丙同底,其顶乙丁相连成甲乙丁丙四边形。形内有甲丁、乙丙两对角线,以此两线相偕为直角形。次以乙丁、甲丙两相对边以甲
乙、丁丙两相对边各相偕为直角形。题言后两形并与前一形等。
其用为:先得五线,以求第六线。〈多罗某之法〉
论球上三角形〈凡二十条〉
凡球上三角形,皆用大圈相交之角。
大测所用三角形之各弧,必小于大圈之半。
球大圈分球为两平,分离于两极,各九十度。
彼大圈过此大圈之极,此两圈必相交为直角。两大圈相交为直角,必彼大圈过此大圈之极。
图
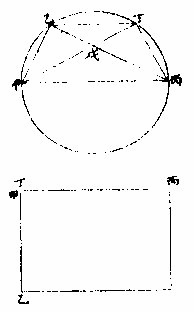
如甲丙大圈,其极乙丁有乙戊丁己大圈过两极,其交处如戊,如己,各成四直角。
球上角之度,必从交引出为两弧,各九十度而遇一象限之弧,两遇处相去之度即此角之大。
如甲乙丙球上三角形,欲
图
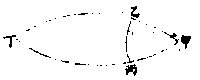
知甲角之大为几何度分,不得用己庚弧为其尺度,必从甲引出至乙、至丙各为一象限之弧。而戊丁亦大圈之一象限弧也。丁戊弧与甲乙、甲丙相遇,即乙丙弧之大为甲角之大。球上角之两边引出之至相遇,即两弧俱成半圈,而
图
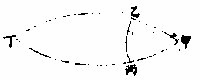
两对角必等。
如甲乙丙三角形,从两腰各引出之至丁,则甲丙丁、甲乙丁两弧皆成半圈,而甲与丁两角等。
球上三角形有相对彼三角形与同底,而对角等,即彼形之两腰为此形两腰之馀腰。
图

初腰不足一百八十度,故后腰为半圈之馀。
其彼此之同方,两角亦等。两直角而彼角为此角之馀角。
如上甲乙丙三角形与相对之乙丙丁同乙丙底,而甲乙两角等,即乙丁为甲乙之馀弧,丙丁为甲丙之
图
馀弧,丁乙丙角为甲乙丙之馀角。
为甲乙丙不足两直角故。
乙丙丁角为甲丙乙之馀角。
球上直角三边形,或有一直角,或二直角,或三俱直角。
图

球上三边形有一直角者,或有两锐角,或有两钝角,或一钝一锐角。
如上甲乙丙形,甲为直角,其乙丙为两锐角。乙丁丙形,丁为直角,其乙丙为两钝角。若丁戊己形则其戊为锐角,其己为钝角。甲戊己形则其戊为钝角;其己
为锐角。
球上直角三边形有两锐角,则其对直角之直角三边形有两钝角。
如前图,甲乙丙之甲直角与乙丁丙之丁直角相对者是。
球上直角三边形有两锐角,其三弧皆小于象限。如前图甲乙丙是。
球上直角三边形有两钝角,其两腰皆大于象限,而第三弧必小于象限。
图

如前图乙丁丙是。
球上直角三边形有一锐一钝角,其锐角之相对三角形亦有一直角、两锐角,如上图丁乙丙三边形,丙为直角,丁为锐角,乙为钝角,即丁锐角之相对乙丙戊形,其丙为直角。
与乙丙丁并等两直角,
图
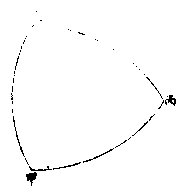
其乙与戊为两锐角。球上三边形有多直角,其对直角之各弧皆为一象限。
如甲为直角,乙丙弧对之为一象限。馀二同。
此图为三直角,题言多者,以该二直角也。
球上三边形有二直角,若
图
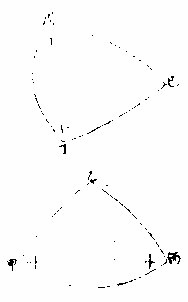
第三为锐角,即对角之弧小于象限。若钝角,即对角之弧大于象限。
如上丁戊己形丁戊皆直角,己为锐角,即对己之丁戊弧小于象限。甲乙丙形甲丙皆直角,乙为钝角,则对角之甲丙弧大于象限。球上斜三角形有三类:或
图

俱锐角,或俱钝角,或杂锐钝角。
球上斜三角形俱锐角者,其相对三角形有两钝角,一锐角。
如上甲乙丙形三皆锐角,即相对丁乙丙形其乙丙为两钝角,丁为锐角。球上三边形俱钝角者,其
图
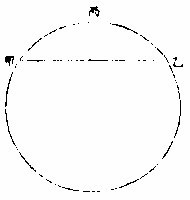
相对三角形有两锐角,一钝角。
如上甲乙丙形三皆钝角,即相对乙丙丁形其乙丙为两锐角,丁为钝角。球上三角形之三角并,大于两直角。
有二直角即大,何况一直一钝以上。
割圆篇第二
总论〈凡二十六条〉
三角形有六率:三角、三边是也。测三角形者,于六率中先得其三,而测其馀三也。
测三角形者,止测其线,非测其容。测或作推,或作解,下文通用。
测三角形必藉同比例法。〈亦曰三率法〉同比例者,四率同。比例先有三而求第四也。故三角形之六率,其比例欲定,其分数欲明。
三角形六率之比例,其中用弧者,最为难定。何者圆线与直线之比例,从古至今未有其法。故
三角形何以有弧。曰:球上三角形其三边皆弧也,其三角皆弧角也。即平面三角形,其可以直线测者,三边耳。欲测其角,非弧不得。而弧为圆,线无数可测。故测弧者,必求其与弧相当之直线。
与弧相当之直线者,割圆界而求其直线之分,与弧分相当者是也。
割圆之直线有四:一曰弦,一名通弦,二曰半弦,皆在
图
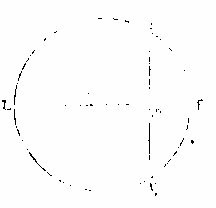
圆界内。三曰切线,在圆界外。四曰割线,在圆界之内外。
弦者,直线在圈内,从此点至彼点分圈为两分。凡弦皆,对两弧一上一下。如上图甲乙为弦,分甲丙乙丁圈为两分,甲丁乙为大分,甲丙乙为小分。则甲
图

乙弦上当甲丙乙小弧,下当甲丁乙大弧。
正弧者,从弧作垂线至全径上。
如上图从丁作甲乙之垂线,若从丁直至戊则为通弦,故丁丙为半弦。
半弦又有二种:有正弦,有倒弦。
图

正半弦是直线在半圈内,从弧作垂线至径上,分半圈为不等之两分,一大弧,一小弧。此半弦者,当小弧,亦当大弧。
当者,为小弧之半弦,亦为大弧之半弦。
如上图从己弧下至甲乙全径,上作己庚垂线,分甲
丙乙半圈为不等两分:乙己弧为小分,己丙甲弧为大分。则己庚为己乙小弧之半弦,又为己丙甲大弧之半弦。
正半弦从一点作两半弦。第一为前半弦,第二为后半弦。又为馀弧弦,又为较弦,又为差弦。
如前图先论,己庚即为前半弦,其己戊即为后半弦。又为馀为较者,乙己丙弧九十度。乙己不足九十度,则己丙为馀弧,亦为较弧。故己戊为馀弦较弦也。前后两半弦,其能等于半径。
图

如上图庚己为前弦当乙己弧,己戊为后弦当己丙馀弧。戊己弦等于丁庚。〈几何一卷三十四〉则丁己半径上方与庚己己戊上两方并等,故云两半弦之能等于半径。
论曰:其两半弦可互为垂线,则己庚丁为直角,而对
图

直角之弦己丁上方与句股上两方并等也。〈几何一卷四十七〉
系直角三边形内有半径,亦有一半弦,即可求后半弦。
法曰:半径上方形实减半弦上方形实,其较即后半弦上方形之实。开方得后
图

半弦。
如丙乙半径十,甲乙前半弦六,而有丙甲乙直角,今求丙甲后半弦。其法:丙乙自之为百,甲乙自之为三十六,相减馀六十四,即甲丙方之实平方法,开之得八。
两正弦之较与纪限左右
图

距等,弧之半弦等。〈六十度为纪限〉解曰:甲乙丙象限内有丙己小弧,丙己戊丁大弧,丙戊弧为六十度,而戊己戊丁两弧等其两半弦:一为己辛,一为丁庚。两半弦之较为丁癸。题言:丁癸较与己壬半弦壬丁半弦各等。论曰:试作一己子线,则丁
己子成三边等角形,何也。此形中有子丁壬、壬己子两三角形,此两角形等,又何也。子戊同腰而丁壬、壬己两腰等,则丁壬、己壬两直角亦等,而丁子、子己两底亦等,子丁己、子己丁两角亦等。又丙戊弧既六十度,其馀戊乙弧必三十度,其乙甲戊角为三十度角。甲乙庚丁既平行,甲戊线截二线于子,即内外角等。而丁子戊角亦三十度,戊子己角亦三十度,是丁子己为六十度角也。丁与己与全子三角既等,两直角〈一卷三十二〉则共为一百八十度。于中减全子角六十度,
图
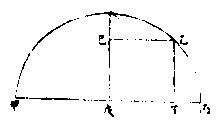
则丁、己两角百二十度。而此两角既等,即各得六十度,则此形之三角三边俱等。夫丁己、巳子两线等,则己癸垂线所分之丁癸、子癸两直角亦等,而己癸同腰则丁癸与癸子必等。丁癸为丁子之半,丁壬为丁己之半,全线等则所分必
等。是丁癸与丁壬等,与壬己亦等。
系题两弧各有其正半弦,两半弦至弧之点在六十度之左右,而距度点等其前两正半弦之较,即后两半弦。
如前图,丙己戊弧六十度,丙己弧五十度,己戊弧十度,丙己之正半弦己辛,简表先得七千六百六十。丙丁弧七十度,丁戊弧亦十度。丙丁弧之正半弦为丁庚,先得九千三百九十六,今求丁戊弧之半弦。其法:以己辛、丁庚两半弦相减得丁癸,较一千七百三十
图

六,即丁戌弧十度之丁壬半弦。〈此设数半径一万〉倒弦者,馀弦与全数之较,本名为矢。
如上图,甲丙径以乙丁正半弦,分径为二:分一为甲丁,一为丁丙。其丁丙即乙丁,正半弦之倒弦也。矢有二,有大有小。
如前图:甲丁为大矢,与甲乙弧相当。丁丙为小矢,与乙丙弧相当。
矢加于馀半弦即半径。
如前图,乙己为乙丁正弦之馀弦以加丁丙,即半径为乙己,与丁戊等故。
切线者,弧之外有线,为径一端之垂线,半径为底线而交于截弧之弦线。
弦线者,句股之弦,非弧矢之弦也。
如上图,戊丙弧乙丙为半径,从丙出垂线至丁,又从
图
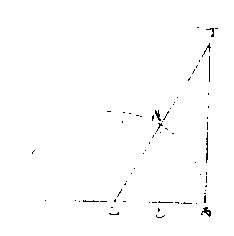
乙出线截戊丙弧于戊,而与丁丙线交于丁。即丁丙为切线,而与戊丙弧相当也。
割线者,从心过弧之一端而交于切线。
如上图,乙戊丁线为割线,与戊丙弧相当也。故戊丙弧在三角形内。其句为半
图

径,其股为切线,其弦为割线,皆与戊丙弧相当之直线。
又戊丙一弧,其相当之直线有四:一丁丙切线,一乙丁割线,一戊己正半弦,一己丙矢。
定割圆之数当作割圆线,以立成表。
图

一名三角形表,一名度数表,今名大测表。
大测表不过一象限。
古用弦则须半周。
如上图用弦,则乙丙弧必得乙丙弦,乃至乙庚弧必得乙庚弦。故百八十度之弧,必得百八十度之弦也。因此术既繁且难,后从简
图

便。则以半弦当之为各半弦,可当上下两弧,故不过一象限而足也。
如上图辛壬半弦当乙壬小弧,亦当壬己甲大弧。庚己半弦当乙己小弧,亦当己甲大弧。且一象限之外无切线,而亦无割线,故用半圈之全不如象限之半
也。
大测表不止有各弧之各度数,亦有其各分数。
欲极详,亦可析分为十,为六也,但少用耳。
作大测表,先定半径为若干,分愈多愈细。
凡割圆四线,大抵皆不尽之数。无论全数不尽,即以畸零法命其分,亦不能尽。故大测表不得谓其不差。但所差甚少,不至半径全数中之一耳。
假如半径为千万,表中诸线中不至差千万分之一分。自一以内或半,或大,或少,不能无差而微乎微矣。故作表中半径必用极大之数,最少者,一万以上或至百万千万,或至万万可也。
七位即千万,八位即万万。
定半径之全数,即可求一象限内各弧各度分之半弦。以此半弦可求得其切线、割线。
凡半径用数少即差多。
如用千则差千之一,用万则差万之一。
用极大之数,即难推。
如用万万以上数,极繁矣。
今定为几何,则可曰:凡半径之数,其中之小分与半弧度分之小分大约相等,而上之即是中数。
假如欲测有分之弧,问半径应定几何。分曰一象限九十度,每度六十分,则一象限五千四百分。又古率圆与径之比例大略为二十二与七,则象限弧与半径之比例若十一与七。
如左图,周二十二四分之,则一象限为五又半。径七二分之,则三又半。此二比例有畸零之数,故各倍之为十一与七也。
图

今用同比例法:〈即三率法〉以象限十一为第一数,以半径七为第二数,以象限五千四百分为第三数,而求得第四数为三千四百三十六。故半径分为三千四百三十六,则半径之各分略相等于一象限之各分,五千四百也。故用大数最少,
图
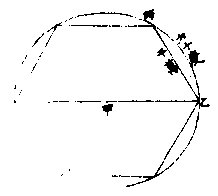
一万为与五千相近。用此乃可推有分之弧也。欲推弧分之秒,亦用此法。其象限为三十二万四千秒。依三率法,十一与七若三十二万四千与二十○万六千一百八十二。其半径细分,与象限之分秒相等,而上之必用百万。
表原篇第三
表原者,作表之原本也。测圆无法,必以直线。直线与圆相准不差,又极易见者,独有六边一率而已。古云:径一围三是也,然此六弧之弦,非六弧之本数。自此以外,虽分至百千万亿,皆弦耳。故测弧必以弦,弦愈细数愈密,其法仍由六边之一准率始。自此又推得五率,此六率皆相准不差。但后五率其理难见,推求乃得是名。为六宗率其法:先定半径为若干数,〈今用一千万〉则作圈内六种多边形。〈俱见几何第四卷〉推此六形各等边之数得此六数,即为六通弦,各当其本弧。因以为作表原本。
宗率一 圈内六边等切形求边数
几何原本四卷十五题言六边等形在圈内者,其各边俱与半径等。半径既定为千万,即边亦千万。凡边皆弦也。圈分三百六十度,此各弦相当之弧各六十度,各与千万相当矣。相当者千万,即六十度弧之弦也。
如左,乙丙圈内有六边等形,其半径甲乙既定为千
图
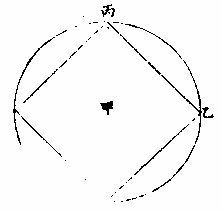
万,即乙丙弦为六边形之一边,亦千万。而相当之乙丙弧六十度。
宗率二 内切圈直角方形求边数
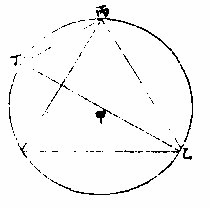
几何四卷第六言:一线在圈内对一象限为方形边,其上方形等于两半径上方形并,〈几何一卷四七〉此句股法
图
也。故用两半径之实,并而开方而得本形边。
如上乙丙圈内方形,甲乙为半径。句股法:甲乙、甲丙上两方并,与乙丙上方等。即以之开方而得乙丙边,今两半径上方形并为二○、○○○○、○○○○、○○○○○。
此数为二百万万万。○旁作点者,万也。末○为单数。
以开方得其边一千四百一十四万二千一百九十六,此为乙丙弧之弦也。乙丙弧为四分圈之一九十度,则乙丙弧数为乙丙九十度弦相当之数。
宗率三 圈内三边等切形,求边数
几何十三卷十二题言三边等形内切圈,其各边上方形三倍于半径上方形。
丁乙方与丙丁、丙乙两方等,而四倍于丙丁形。则
图
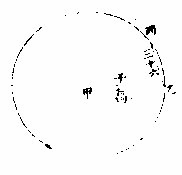
丙乙为丁乙四之三,而三倍于丙丁。
如上图,乙丙圈甲乙为半径,乙丙上方三倍大于甲乙上方,即三因半径上方为三○、○○○○、○○○○、○○○○○。
此数为三百万万万有奇。
图

开方得一千七百三十二万○五○八弱。
宗率四 圈内十边等切形求边数
几何十三卷九题言:以比例分半径为自分,连比例线,其大分则十边等形之一边。
如上图,甲乙半径与戊己
图

等,用自分连比例法。
几何六卷三十称理分中末线
分为大小分。其大分为丁己,与十边形之乙丙边等。盖戊己线与己癸等,己癸线既两平分于庚,则戊己己庚线上两方并,与庚戊上方等。〈几何一卷四十七〉今以庚
戊上方开得庚戊线为一千一百一十八万○四百三十○。次减去己庚五百万馀六百一十八万○四百三十○,即丁己线,亦即乙丙弦。而乙丙弦为全圈十分之一,得三十六度,是乙丙为三十六度弧之弦。
宗率五 圈内五边等切形求边数
几何十三卷第十题言:圈内五边等切形,其一边上方形与六边等形、十边等形之各一边上方形并等也。
如左圈内,甲乙戊为五边等形,甲丙己为六边等形,
图
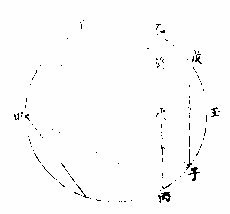
甲丁乙为十边等形。题言:甲丁、甲丙上两方并,与甲乙上方等者,前言甲丙半径为千万,甲丁线为六百一十八万○四百三十○,各自之,并得数开方,得甲乙线为一千一百七十五万五千七百○四弱。其弧五分全圈得七十二,即甲
乙为七十二度弧之弦。
宗率六 圈内十五边等切形,求边数。
几何四卷十六题言,圈内从一点作一三边等形,又作一五边等形。同以此点为其一角,从此角求两形相近之第一差弧,即十五边形之一边。
如左图,从甲点作甲乙丙三边形,甲丁戊五边形,求得两形相近之第一差为乙戊,即十五边等形之一边,乃丁乙全差之半。其数先有三边形之乙丙,一百二十度之弦为一千七百三十二万○五百○八弱。
图
又有五边形之戊子,七十二度之弦为一千一百七十五万五千七百○四弱。则乙庚六十度之正弦为乙丙之半,得八百六十六万○二百五十四弱。戊辛三十六度之正弦为戊子之半,得五百八十七万七千八百五十二。两相减馀
为乙癸,得二百七十八万二千四百○二。夫乙己半径上方减壬乙六十度之正弦,乙庚上方馀己庚。依开方法为五百万。己子半径上方,与己辛三十六度之正弦辛子上两方并等。依前法亦得己辛八百○九万○一百七十○。己辛、己庚两相减馀为庚辛,得三百○九万○一百七十○,庚辛即戊癸也。既得乙癸二百七十八万二千四百○二,今得戊癸三百○九万○一百七十○,用句股术求得乙戊弦为四百一十五万八千二百三十四,为十五边等形之一边。其乙戊弧为全圈十五分之一,得二十四,则乙戊为二十四度弧之相当弦。
六题总表
边 弧度 弦数
三 一百二十 一七三二○五○八四 九十 一四一四二一九六五 七十二 一一七五五七○四六 六十
十 三十六 六一八○三四○十五 二十四 四一五八二三四既得全数,今推半弧、〈即半角〉半弦。
弧度 半弦
六十 八六六○二五四
四十五 七○七一○九八
三十六 五八七七八五二
三十 五○○○○○○
十八 三○九○一七○
十二 二○七九一一七〈以上原本卷一〉